Trajectory of a photon in a moving box

[flexible_time]

I have a basic question about the trajectory of a photon.

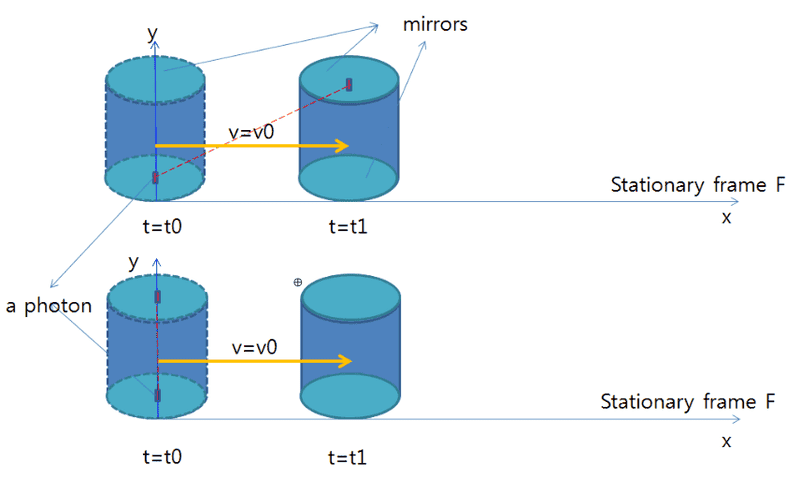
As can be seen in the figure above, let's suppose there is a stationary frame F and a cylinder sealed with two sided mirror is located at the origin of F. Then let's consider two cases; First is the velocity of cylinder is 0 with regard to F and second is constant v=v0. For the first case, at initial time t=t0, single photon is emitted from the center of bottom mirror to the positive y direction with velocity c so that the x position of the photon is not changed. Because of zero velocity of cylinder, the photon will bounce off from side to side forever so the trajectory of the photon will be like the red dotted line at bottom of the figure. So far so good.

Here comes my question concerning the second case v=v0. If the velocity of cylinder with regard to F is non-zero v0 and travel from x=0 to x=v0*(t1-t0), then what will the trajectory of the photon look like? the diagonal path or path parallel y-axis of F? Is the x position of the photon 0 or v0*(t1-t0) at t=t1? Which one is correct?

According to the link here, the answer seems to be x=v0*(t1-t0) when measured in frame F. Do I understand correctly? If so, I doubt where does x changes come from although the photon is emitted to a perpendicular direction to the x axis?

 

[Nugatory]

f so, I doubt where does x changes come from although the photon is emitted to a perpendicular direction to the x axis?

This is the same problem as bouncing a ball up and down on the deck of a ship. An observer on the ship sees the ball moving straight up and down with no horizontal component while an observer on the dock watching the ship move slowly by sees the ball following the slantwise path with some velocity in the x-direction. (We can do it the other way as well: the dockside guy bounces a ball straight up and down on the dock; ship guy, believing himself to be at rest while the dock slips slowly backwards will see the ball following a slanting path).

The path of the ball through space is the same whether viewed by dock guy or ship guy - the ball moves through the same points in space either way. The apparent horizontal velocity is introduced by the arbitray choice we've made about what's moving horizontally and what's not.

(As an aside: You should get in the habit of thinking "flash of light" or "light pulse" or "light signal" instead of "photon". Photons aren't what you think they are, and there's no such thing as a photon traveling on a path like you're describing. Fortunately this doesn't change anything in this problem - the question makes just as much sense with a flash of light).

 

[flexible_time]

The path of the ball through space is the same whether viewed by dock guy or ship guy - the ball moves through the same points in space either way.

Thank you for reply. So does it mean that the flash of light will be detected at x=v0*(t1-t0) at t1 in frame F? My understanding is the speed of light is constant c and since t=t0, the flash of light have already 100% speed of c along y-axis and no room left for velocity for x direction. If the y portion of velocity of light is c when measured in frame F all the time being till reaching top mirror, then it seems to be impossible for light to gain more speed along x-axis because it means moving faster than the speed limit c.

 

[Nugatory]

Thank you for reply. So does it mean that the flash of light will be detected at x=v0*(t1-t0) at t1 in frame F? My understanding is the speed of light is constant c and since t=t0, the flash of light have already 100% speed of c along y-axis and no room left for velocity for x direction. If the y portion of velocity of light is c when measured in frame F all the time being till reaching top mirror, then it seems to be impossible for light to gain more speed along x-axis because it means moving faster than the speed limit c.

Both observers must agree that the speed of light is $c$. Both observers can calculate the distance the flash of light must cover to get from one mirror to the other, and they will come up with different results (if the two mirrors are separated by one meter in the y direction, the distance is $\sqrt{1+\Delta{x}^2}$ and $\Delta{x}$ is zero for the observer at rest relative to the box, non-zero for the observer moving relative to the box).

But if the speed is the same and the distance traveled is different, then the travel time must be different... and we've just discovered relativistic time dilation! This two-mirror device you are studying is actually an idealized clock (it's often called a "light clock", and you will find many threads discussing it here). We can say that one tick of the clock corresponds to one mirror-to-mirror passage; if we place the mirrors one light-second apart our clock will even nicely tick once every second. But as the analysis above shows, the clock that is moving relative to us will tick more slowly than the clock that is at rest relative to us.

 

[pixel]

(As an aside: You should get in the habit of thinking "flash of light" or "light pulse" or "light signal" instead of "photon". Photons aren't what you think they are, and there's no such thing as a photon traveling on a path like you're describing.

Can you elaborate on this?

 

[Vitro]

Can you elaborate on this?

The photon is a quantum object who's behavior is best described by quantum electrodynamics. It does not travel along a path in the classical sense, it is emitted at some place and time (event A) and can be detected at some other place and time (event B) with some probability. One cannot answer (or even ask) how it gets from A to B or where it is at some intermediate time. That's my limited understanding of it.

 

[Nugatory]

Can you elaborate on this?

There are many posts on this topic over in the quantum physics subforum. If you have further questions after reading some of them, you should start a thread there.

 

[flexible_time]

(if the two mirrors are separated by one meter in the y direction, the distance is $\sqrt{1+\Delta{x}^2}$ and $\Delta{x}$ is zero for the observer at rest relative to the box, non-zero for the observer moving relative to the box)

I already guessed your answer but the problem for me is that I cannot accept easily that $\Delta{x}$ is non-zero in frame F. Let me explain more my frustration.

There are two events; First is the emission of light at t=t0 and second is the detection at y=h assuming h is the height of box measured in the stationary frame F. At t=t0, light is emitted in the positive y direction with velocity c. This event should be agreed on both frame F(stationary frame) and F'(box frame) but let's stick to the frame F only and forget about box frame. It seems to be obvious to me that the velocity of light is $0x+cy$ at t0 and it is my belief that there is nothing external to change the path of emitted light especially in x direction of frame F. If $\Delta{x}$ is non-zero as you wrote, that means any observer stationary relative to frame F must be able to measure the non-zero velocity of light in x direction but this conclusion seems to be violated with the initial assumption that light is emitted with the velocity $0x+cy$. So I believe that if the velocity of light is $0x+cy$ at t0 in frame F, then $\Delta{x}$ must be zero in frame F because initial velocity of light in x direction is zero and no external force to change x position of flash of light. What is wrong with my understanding?

 

[Nugatory]

What is wrong with my understanding?

The light source is moving in one frame but not the other. Light leaves a moving source at a different angle than a stationary one, so there's no reason for the x components of the velocity to be the same in both frames. That bit about different angles may sound bizarre at first, but it's actually quite natural: consider the example of the ball bouncing up and down on a moving ship. In one frame the deck isn't moving and the trajectory of the ball is perpendicular to the deck; in the other frame the deck is moving and the trajectory of the ball makes an angle with the deck.

Another way of thinking about it: the flash of light follows the same path through space in both frames. Imagine that the space between the mirrors is full of fine dust. Every grain of dust is at rest relative to one of the observers (so is moving relative to the other). As the light moves through the dust it illuminates each individual grain as it reaches it. Both observers agree about which individual grains are illuminated... But the line we draw through the illuminated grains will be slanting in one frame and vertical in the other because the grains are moving in one frame and not the other.