- #1
mlb2358
- 16
- 0
Hi Everyone,
I'm having some trouble with a problem concerning translational and rotational equilibrium. The question involves a balance with various masses suspended from it (see attached image). The question states that the counterweight is moved from 1cm away from the fulcrum to 2cm away from the fulcrum and asks whether or not the rod is still under rotational and translational equilibrium. I understand that it is no longer in rotational equilibrium because there is now a net torque acting on the rod, however the translational equilibrium portion is unclear to me. The answer argues that the masses suspended from the rod no longer exert the same force on the rod because they are now accelerating, thus translational equilibrium is no longer present. I am unclear as to why they are accelerating. I realize that the apparatus will rotate which gives it angular acceleration, but is this enough to conclude that it has linear acceleration as well (alpha =a/r)? If this is the case, how could we ever have have translational equilibrium while not having rotational equilibrium?
I'd appreciate any help, thanks.
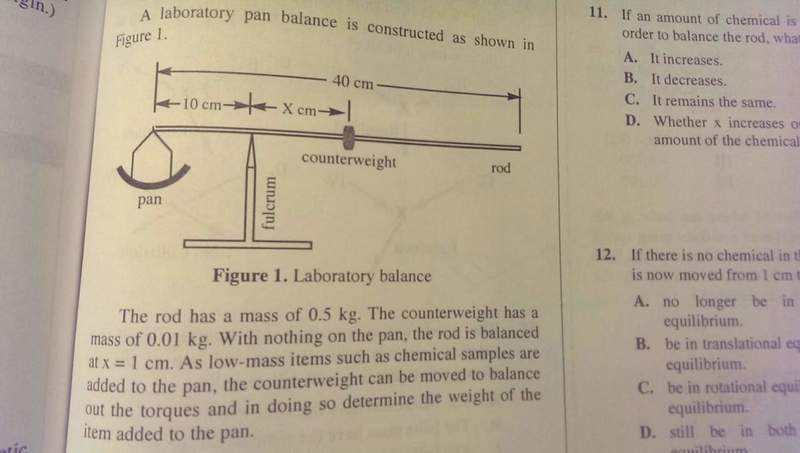
I'm having some trouble with a problem concerning translational and rotational equilibrium. The question involves a balance with various masses suspended from it (see attached image). The question states that the counterweight is moved from 1cm away from the fulcrum to 2cm away from the fulcrum and asks whether or not the rod is still under rotational and translational equilibrium. I understand that it is no longer in rotational equilibrium because there is now a net torque acting on the rod, however the translational equilibrium portion is unclear to me. The answer argues that the masses suspended from the rod no longer exert the same force on the rod because they are now accelerating, thus translational equilibrium is no longer present. I am unclear as to why they are accelerating. I realize that the apparatus will rotate which gives it angular acceleration, but is this enough to conclude that it has linear acceleration as well (alpha =a/r)? If this is the case, how could we ever have have translational equilibrium while not having rotational equilibrium?
I'd appreciate any help, thanks.