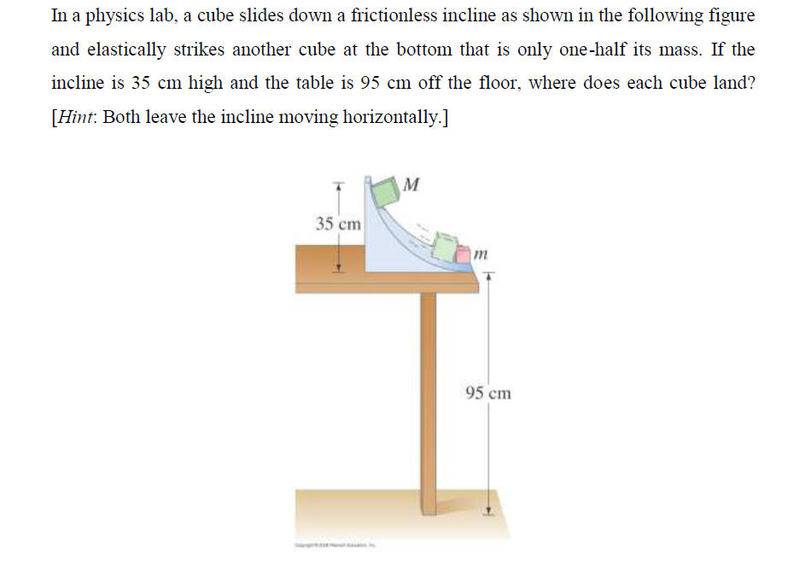
SUMMARY
The forum discussion centers on solving a physics problem involving energy conservation and elastic collisions. Key equations discussed include gravitational potential energy (PE = mgh), kinetic energy (KE = 1/2mv²), and momentum conservation equations. Participants emphasize the importance of recognizing that mass cancels out in the equations, allowing for simplification. The final velocities derived from the equations are v₁ = (1/3)√(2gh) and v₂ = (4/3)√(2gh), which are confirmed as correct solutions.
PREREQUISITES
- Understanding of gravitational potential energy (PE = mgh)
- Knowledge of kinetic energy (KE = 1/2mv²)
- Familiarity with conservation of momentum principles
- Ability to solve simultaneous equations
NEXT STEPS
- Review the principles of elastic collisions in physics
- Learn how to derive equations for conservation of energy
- Explore the application of kinematic equations in real-world scenarios
- Practice solving simultaneous equations in physics problems
USEFUL FOR
Students studying physics, particularly those focusing on mechanics and energy conservation, as well as educators looking for problem-solving strategies in elastic collisions.