- #1
Qube
Gold Member
- 468
- 1
Summary:: After firing a projectile from the top of a hill, where does it land on the hill? I disagree with the professor in approach and final result.
Problem Statement:
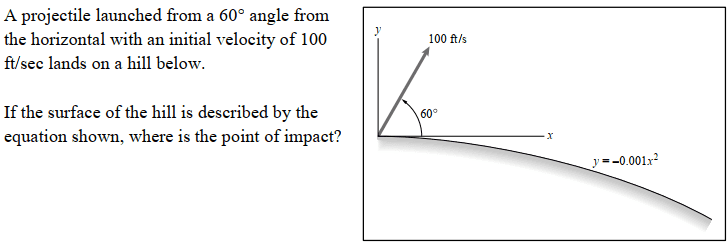
Relevant Formulas:
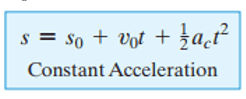
Attempt to Solve:
I'm very familiar with these types of problems. I'm not here for help solving the entire problem. I just have a small point of contention with my professor about finding the final y-coordinate of the projectile.
I am confident that to find the final y-coordinate of the projectile, the correct equation should be:
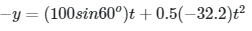
My professor argues that the correct equation is instead:
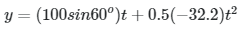
We both agree on the equation for finding the x-coordinate of the projectile.
I disagree with the professor's equation for finding the final y-coordinate of the projectile. Displacement is final position - initial position, and the final y-coordinate is obviously "-y." The initial y-coordinate is obviously 0. The displacement of the particle, therefore, should be "-y" not "y."
Also, solving similar problems in the textbook with the professor's approach results in negative time values.*
Question:
Who's formula is correct in solving for vertical displacement?
----
*Example of me getting a negative time value with the professor's approach:
This is the book's solution; note the "-y."

This is what happens when you decide to solve it with the same equations, but with a "+y":

Finally, this guy seems to have no issue with assuming the sign of the "y" in another similar problem:
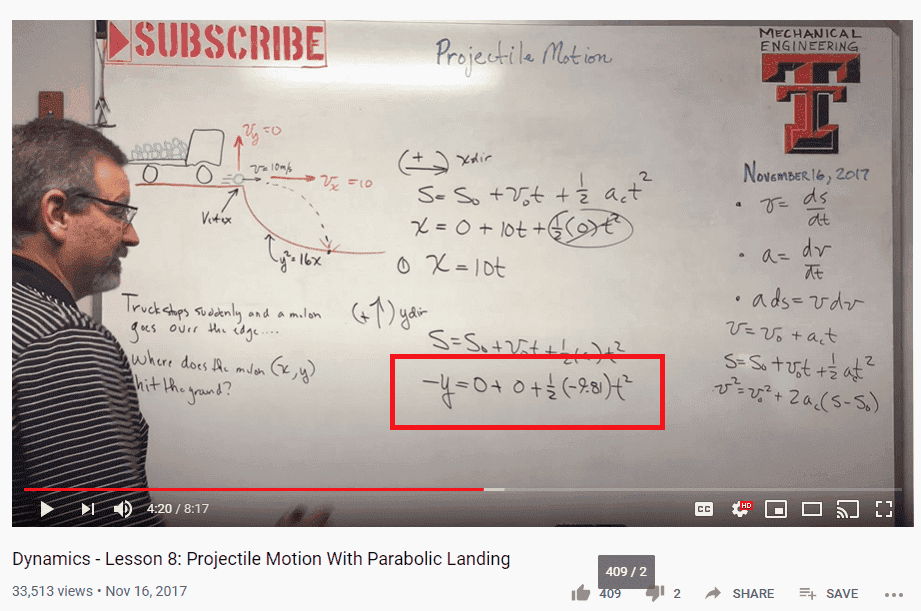
Problem Statement:
Relevant Formulas:
Attempt to Solve:
I'm very familiar with these types of problems. I'm not here for help solving the entire problem. I just have a small point of contention with my professor about finding the final y-coordinate of the projectile.
I am confident that to find the final y-coordinate of the projectile, the correct equation should be:
My professor argues that the correct equation is instead:
We both agree on the equation for finding the x-coordinate of the projectile.
I disagree with the professor's equation for finding the final y-coordinate of the projectile. Displacement is final position - initial position, and the final y-coordinate is obviously "-y." The initial y-coordinate is obviously 0. The displacement of the particle, therefore, should be "-y" not "y."
Also, solving similar problems in the textbook with the professor's approach results in negative time values.*
Question:
Who's formula is correct in solving for vertical displacement?
----
*Example of me getting a negative time value with the professor's approach:
This is the book's solution; note the "-y."
This is what happens when you decide to solve it with the same equations, but with a "+y":
Finally, this guy seems to have no issue with assuming the sign of the "y" in another similar problem:
Last edited: