- #1
physicophysiology
- 12
- 3
<Moderator's note: Moved from a technical forum and thus no template.>
Mechanics by Lev D. Landau & E. M. Lifshitz
Chapter 4 Collisions between particles
§16. Disintegration of particles
Problem 3

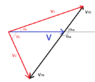
The angle θ = θ1 + θ2
It is simplest to calculate the tangent of θ.
A consideration of the extrema of the resulting expression gives the following ranges of θ, depending on the relative magnitudes of V, v10 and v20 (for definiteness, we assume v20 > v10):
0 < θ < π if v10 < V < v20,
π-θ10 < θ < π if V < v10,
0 < θ < θ10 if V > v20.
So I calculated the tangent of θ and derivative of it
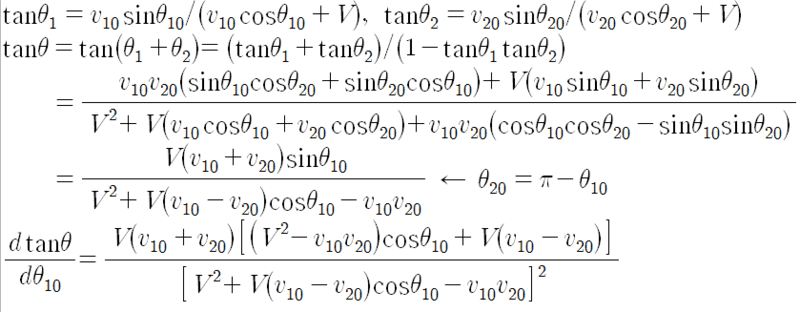
But I can not calculate the extrema, thus I can not solve it...
How to do calculate the extrema?
In addition,
How to do calculate the following?
sinθ10 = V(v10 + v20)/(V2 + v10v20)
Mechanics by Lev D. Landau & E. M. Lifshitz
Chapter 4 Collisions between particles
§16. Disintegration of particles
Problem 3
The angle θ = θ1 + θ2
It is simplest to calculate the tangent of θ.
A consideration of the extrema of the resulting expression gives the following ranges of θ, depending on the relative magnitudes of V, v10 and v20 (for definiteness, we assume v20 > v10):
0 < θ < π if v10 < V < v20,
π-θ10 < θ < π if V < v10,
0 < θ < θ10 if V > v20.
So I calculated the tangent of θ and derivative of it
But I can not calculate the extrema, thus I can not solve it...
How to do calculate the extrema?
In addition,
How to do calculate the following?
sinθ10 = V(v10 + v20)/(V2 + v10v20)
Attachments
Last edited: