Euler2718
- 90
- 3
First I'd just like to point out that I'm taking calculus and advance pre-calculus simultaneously (kind of a stupid system) and this is a problem in the pre-calc.
1. Homework Statement
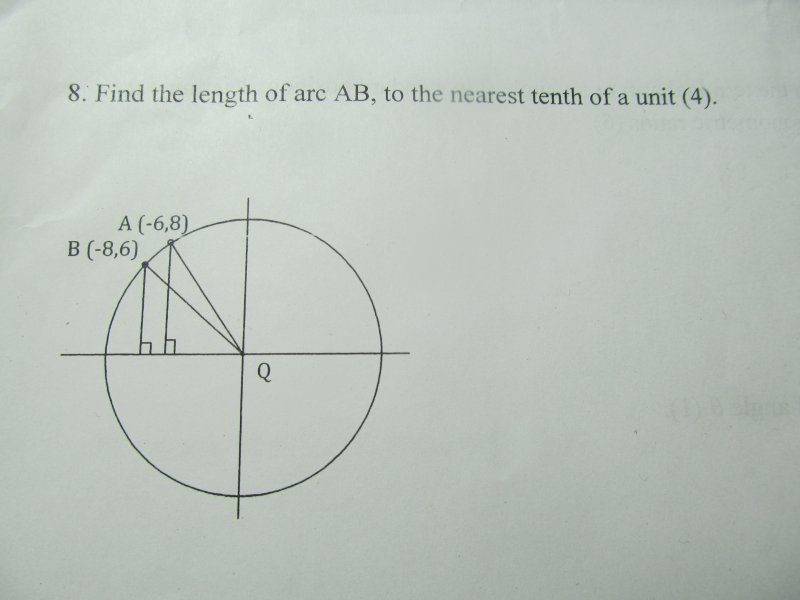
2. Homework Equations
Let 'a' be arc length.
a=\theta r
a = \int_{a}^{b} \sqrt{1+[f'(x)]^{2}} dx
3. The Attempt at a Solution
The lecture on arc length wasn't even a lecture. Merely a hand out of the chapter summery, not to be touched again. I saw no central angle so a=\theta r seems to be out of the question. This seemed to be an unusual problem, so I used Pythagoras after a while. I went
( \Delta x )^{2} + (\Delta y)^{2} = a^{2}
This yields the arc length to \sqrt{8} units.
I confirmed this with the integration for arc length. But I'm really not at the level of arc length integration yet. I can do basic integration only (I skipped ahead in the course a bit). Via wolfram alpha:
\int_{-8}^{-6} 10\sqrt{\frac{1}{100-x^{2}}} dx = 10\sin ^{-1}\left(\frac{7}{25}\right) \approx 2.83794
Which is pretty much \sqrt{8} So really, my question is if there is another more formal way to approach this problem using trigonometric concepts to arrive at an answer.
Thank you in advance.
1. Homework Statement
2. Homework Equations
Let 'a' be arc length.
a=\theta r
a = \int_{a}^{b} \sqrt{1+[f'(x)]^{2}} dx
3. The Attempt at a Solution
The lecture on arc length wasn't even a lecture. Merely a hand out of the chapter summery, not to be touched again. I saw no central angle so a=\theta r seems to be out of the question. This seemed to be an unusual problem, so I used Pythagoras after a while. I went
( \Delta x )^{2} + (\Delta y)^{2} = a^{2}
This yields the arc length to \sqrt{8} units.
I confirmed this with the integration for arc length. But I'm really not at the level of arc length integration yet. I can do basic integration only (I skipped ahead in the course a bit). Via wolfram alpha:
\int_{-8}^{-6} 10\sqrt{\frac{1}{100-x^{2}}} dx = 10\sin ^{-1}\left(\frac{7}{25}\right) \approx 2.83794
Which is pretty much \sqrt{8} So really, my question is if there is another more formal way to approach this problem using trigonometric concepts to arrive at an answer.
Thank you in advance.