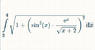Using dy/dx to find arc length of a parametric equation

[Coderhk]

Homework Statement

I have attached a picture of the problem in the attachments

I need help on the last section, (part d)

Homework Equations

(1)$∫√( (dx/dt)^2+(dy/dt)^2)dt$
(2)$∫√( 1+(dy/dx)^2)dx$[/B]

The Attempt at a Solution

In order to get the answer we just need to find the arc-length of the position curve which could be done using the first equation. However, instead of using the first equation I divided $dy/dt$ by $dx/dt$ to find $dy/dx$. Using dy/dx I plugged it into the second equation and got a different answer. Why is that so? Shouldn't they both yield the same answer? For both equations I used from 2 to 4 as the limits of integration.

Thanks[/B]

 

[BvU]

Using dy/dx I plugged it into the second equation and got a different answer

I don't see what you do (not clearvoyant). Please post your attempt in full.

For both equations I used from 2 to 4 as the limits of integration.

And why is that ?

 

[Coderhk]

I don't see what you do (not clearvoyant). Please post your attempt in full.
And why is that ?

I plugged this into a calculator and got 5.975

 

[BvU]

I plugged this into a calculator and got 5.975

Sure. But x starts at 1 and ends at what you (?) found .

And you have an integrand that is a function of t, not of x. So you either need to express dx as a function of t (and then you are back again to the solution manual), or express the integrand as a function of x, which I think is pretty tough.

 

[Coderhk]

Sure. But x starts at 1 and ends at what you (?) found .

And you have an integrand that is a function of t, not of x. So you either need to express dx as a function of t (and then you are back again to the solution manual), or express the integrand as a function of x, which I think is pretty tough.

Wouldn't the limit of integration actually be from 1 to 1.252 (answer from part b), I tried that and I got 0.439. Also, what do you mean by expressing the integrand as a function of x? Isn't it already as a function of x? I just simply plugged it into the formula $∫√(1+(dy/dx)^2)dx$

 

[BvU]

I tried

Can't be: you don't have $t(x)$ yet, so you can't integrate. Your result is simply the result of the wrong integration. And "I" got 0.441251 !?

Isn't it already as a function of x?

It certainly is not: dividing two functions of $t$ does not change the $t$ into an $x$ !

 

[Coderhk]

Can't be: you don't have $t(x)$ yet, so you can't integrate. Your result is simply the result of the wrong integration. And "I" got 0.441251 !?
It certainly is not: dividing two functions of $t$ does not change the $t$ into an $x$ !

Ok, I see what you mean now, the $dy/dx$ is still in terms of t which is why the the integrand is incorrect. Thank you