SUMMARY
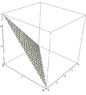
The discussion focuses on evaluating the triple integral of the function xy over a solid tetrahedron defined by the vertices (0,0,0), (10,0,0), (0,8,0), and (0,0,5). The user proposes integration bounds for dy and dx based on the z-axis, suggesting limits of 0 to y = -8z/5 + 8 for dy and 0 to x = -2z + 10 for dx, with dz ranging from 0 to 5. A recommendation is made to first solve the integral using the dzdydx order for clarity, emphasizing the need to compute the equation of the plane at the tetrahedron's top using the cross product to find the normal vector.
PREREQUISITES
- Understanding of triple integrals in multivariable calculus
- Familiarity with solid geometry, specifically tetrahedrons
- Knowledge of vector calculus, including cross products
- Experience with integration techniques in multiple dimensions
NEXT STEPS
- Learn how to compute the equation of a plane using the cross product
- Study the process of evaluating triple integrals in dzdydx order
- Explore the geometric interpretation of triple integrals over solids
- Practice solving triple integrals with varying limits based on geometric shapes
USEFUL FOR
Students and educators in mathematics, particularly those studying calculus and solid geometry, as well as anyone seeking to understand the evaluation of triple integrals over complex regions.