Tube Bending Stress: Hand Calcs vs FEA Analysis

[Saints-94]

I have ran an FEA simulation on a lever to work out the stress on the part. I have now started doing some hand calculations to validate the software results and am struggling to get the values to match up. I am unsure whether my calculations are wrong, or whether the software is incorrect.

The part is a metal tube (below), with a 25.3mm diameter and 2mm wall thickness.

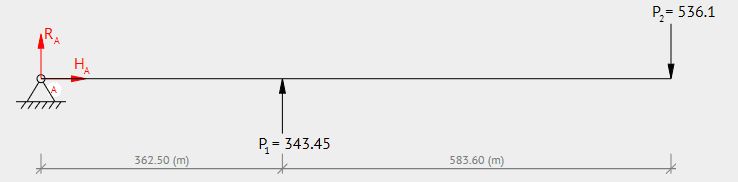
I know that;

Stress = My / I

I have worked my bending moment out as
M(x1) = + RA*(x1) - MA
M1(0) = + 192.65*(0) - 382703.59 = -382703.59 (N*m)
M1(362.50) = + 192.65*(362.50) - 382703.59 = -312867.96 (N*m)

Y= D/2
=12.65mm = 0.01265m

I = (pi * D^4) / 64
= (pi/64) * (0.0253^4 - 0.0233^4)

The answer I have calculated is 7.05 x 10^11 Nm2
and FEA analysis = 2.1 x 10^8 Nm2

Please come someone confirm whether my hand calcs are correct or not?

 

[Dr.D]

If the OD = 25.3 mm, with a 2 mm wall, the ID should be ID = 21.3 mm. This will give you a different result for I.

 

[Saints-94]

Thanks for that, my mistake!

However my calculations are still coming out at 3.955E+11, as opposed to the 2.1E+8.

Seems like they are still quite a bit different, any ideas why this could be?

 

[Mech_Engineer]

Can you clarify, what are the boundary conditions on the beam? Is it simply supported at the left end and an intermediate point, with a load on the right side?

Also make sure you're calculating your section modulus correctly, the formula should be this one:

https://en.wikipedia.org/wiki/Section_modulus#Elastic_section_modulus

 

[JBA]

The reaction force at A to balance P1 and P2 for the simple hinged connection at that point in your diagram cannot be reconciled with the P1 and P2 loads shown because the torques about A are not balanced without a compensating torque about point A. Is end A a hinged or rigid cantilever support?

 

[Dr.D]

This is a tube almost 1 km in length, with an OD of approximately 1 inch? Really? I would think you need to include the weight of the tube in your calcs as well.

 

[JBA]

I had totally missed the above mix of length vs pipe size. If this is a "hand lever" as described the lengths or their units are in error.

Should those be mm instead of m? If so they would be in USA units: 14.27 in. and 22.9 in. respectively.

 

[Saints-94]

Thanks for all your responses.

Apologises, I got my units mixed up! It should read mm, not m. The lever is a fixed hinge on the left hand side.

My bending moment has be re-calculated as..
M(x1) = + RA*(x1) - MA
M1(0) = + 192.65*(0) - 382.70 = -382.70 (N*m)
M1(0.36) = + 192.65*(0.36) - 382.70 = -312.87 (N*m)

Then,

Y= D/2
=12.65mm = 0.01265m

I = (pi * D^4) / 64
= (pi/64) * (0.0253^4 - 0.0213^4)

Stress = My / I
=3.955E+08

This is a lot closer to my FEA results ( 2.1 x 10^8 Nm2), would you say this discrepancy is acceptable?

 

[Dr.D]

Looks like you are still off by a factor of 2. I don't know what your acceptance criteria are, but that's not very close in my book!

By the way, what is a "fixed hinge"? Does it allow rotation or not? As drawn, it looks like a built-in support.

 

[Saints-94]

I was expecting them to be closer, that's why I was concerned I had calculated it wrong.

Yes, it allows it to rotate

 

[Dr.D]

If the left end hinge is truly a hinge (rotation allowed), then the bending moment is zero at that point and your first equation for M(x1) is wrong. I think it goes downhill from there.

Additionally, the system is not in rotational equilibrium with the loads shown, so statics does not apply.

 

[JBA]

Clearly way too much error. At the same time, in the above diagram you are definitely not showing an accurate repersentation for a handle with a pivot at A and a downward force of 536.1 ?units at P2.

If the left connection is a pivot or hinge then there is no bending moment at that location only a reaction force and shearing stress.

Where or how are you getting your two loads shown on your diagram?

If this is a handle with a pivot at A with a downward force at P2 pressing on an object at P1 then your assumed reaction force at P1 is in error because the moments about A do not balance.

 

[Saints-94]

The two forces have been found through research.

The lever is on a hinge at the left, P2 is a human downward pull force, and P1 is where an object is being compressed.

The moment I have used in the stress calculation is M1(0.36), as this is where I believe the stress will be acting(?) So for my stress equation I used 312.879(N*m), for M.

M(x1) = + RA*(x1) - MA
M1(0) = + 192.65*(0) - 382.70 = -382.70 (N*m)
M1(0.36) = + 192.65*(0.36) - 382.70 = -312.87 (N*m)

 

[JBA]

One more question, is the handle pivot/hinge at A a free rotating pin or does it have some spring or torsion bar that imposes a counter clockwise torque on the pin and handle at that point.

 

[Saints-94]

There is a hook on the lever at point A, which is to attach to a bar. The lever can pivot on this point around the bar. Therefore this has been treated as a hinge.

 

[JBA]

Thank you for the picture, based upon this it can be said that the A point is a free rotating hinge; and, due to the handle design, under load there will be a bending moment created in the handle hook either in the region between the the pin contact point and the transition taper to the full thickness of the lever if the reaction force is downward on the pin or along any point of the hook if the reaction force on the pin is upward (as would be a expected based upon the loadings shown). If you are to match your calculation result to that of the FEA in this segment of the handle it is going to be critical that you identify the exact location along that section that the FEA is using as the point of reference for its value.

With that issue resolved, I this have some concern about your model's applied loads for the following reason:

By using a simple statics analysis for the handle as a lever with A as the hinge point, the P2 = 536.1 N load at (.36 + .58) = .94 mm is going to result in a P1 reaction force = 536.1 N *(.94 / .36) = 1399.8 N which far exceeds the 343.45 N force at P1 that you say is determined by research; or alternatively,

If the force at P1 = 343.45 N then the handle force at P2 required to create that reaction force is 343.45 * (.36 / .94) = 131.5 N which is well below the 536.1 N on the diagram. So it appears that something is clearly missing in either the model or the data used to create the model.

 

[Saints-94]

Thanks again for your help.

I have realized that I needed to half both forces as the lever is made up of two 'beams'.

This then gives me a moment of;
M1(0) = + 96.35*(0) - 191.39 = -191.39 (N*m)
M1(0.36) = + 96.35*(0.36) - 191.39 = -156.46 (N*m)

Which gives me a stress of
1.978E+08. This seems closer to my software analysis now.

How did you work out the reaction at point P1?

 

[JBA]

It is a simple matter of the ratio of forces and the lengths of those points from a given pivot point, as an example, if I have a lever, like the one in your problem, that is L2 = 2 m long with a pivot A at one end and a point on the beam P1 that is L1 = 1 m from the pivot end of the beam, and I push down with F2 = 10 N of force at L2 = 2 m at the P2 end of the beam then the resulting applied force on an resisting object at P1 will be F1 = F2 * (L2 / L1) = 10 N * (2 m / 1 m) = 20 N.

In all cases: F1 * L1 = F2 * L2 (Of course, as shown in your model, from the beam's standpoint: F1 * L1 = - F2* L2 )
(The ratio of those forces is locked by the ratio of their distances from the pivot, so, if you change one of those forces then the other is automatically changed as well)

I hope this helps answer your question

 

[Saints-94]

Thanks for your help.

I was wondering if you could help me work out deflection at P2?

 

[JBA]

For this your handle can be treated as a beam with a hinge at A, an intermediate support at P1 and a downward force F2 applied at point P2 that is divided by 2 to provide the the equal deflection on each of the two handle side pipes. The P1 point reaction force is not required for this analysis because, as I explained above, the reaction force at P1 is inherently established by the ratio of the P1 and P2 lever lengths from A.

Next, I (moment of inertia) = .049* D^4 - d^4) for the pipe used on the handle and E (Modulus of Elasticity) for the pipe material is needed.

With those values then the formula for the deflection at the handle end P2 is: y = (F2 / 2) * .58^2 * (.58 + .36) / (3 * E * I)

Note: This beam configuration and the y deflection equation for this beam configuration is given in the "Machinery Handbook", Table of Stresses and Beam, Case 8.; and at: http://www.engineersedge.com/beam_bending/beam_bending6.htm

(Where your lever is a special case with no overhang beyond the end opposite from the end where the W load is being applied; but, the lack of an overhang at that opposite end has no effect upon the calculation of the deflection at the loaded end of the beam.)

 

[Saints-94]

Thanks. I have put these into the formula and have got..

Moment of inertia;
I=(π×D^4)/64

I=π/64×(〖0.0253〗^4-〖0.0213〗^4)

I=1.000797×〖10〗^8 m^4
W;
W=F2/2

W=268.05/2

W=134.03N
Deflection;
y=(Wc^2)/3EI(c+l)

y=(134.03×〖0.58〗^2)/(3×(7.03×〖10〗^10)×(1.000797×〖10〗^8))(0.58+0.36)

y=0.0201

Note: The modulus of elasticity for the aluminium is 70.3GPa (converted to (7.03×〖10〗^10)N/m2)

I am unsure whether this is correct and whether i have used the right units?

In my software simulation i got a deflection of 7.93mm.

 

[JBA]

You need to revise your analysis model to match our computational one in which P1 is a simple vertical support point.

P2 can be entered as a reaction force, but the FEA result indicates to me that you may not have used the correct reaction force at P1; which as discussed before is fully dependent upon the P1 x L1 = P1 x L2 discussed and (as indicated by my earlier ratio calculation given below) should be for one side of the handle:
F1 @ P1 / 2 =1399.8 N / 2 = 699.54 N.

Regardless of that the best method of modeling the arm reaction point at P1 in the FEA analysis is still as a simple vertical support point.

By using a simple statics analysis for the handle as a lever with A as the hinge point, the P2 = 536.1 N load at (.36 + .58) = .94 mm is going to result in a P1 reaction force = 536.1 N *(.94 / .36) = 1399.8 N"