SUMMARY
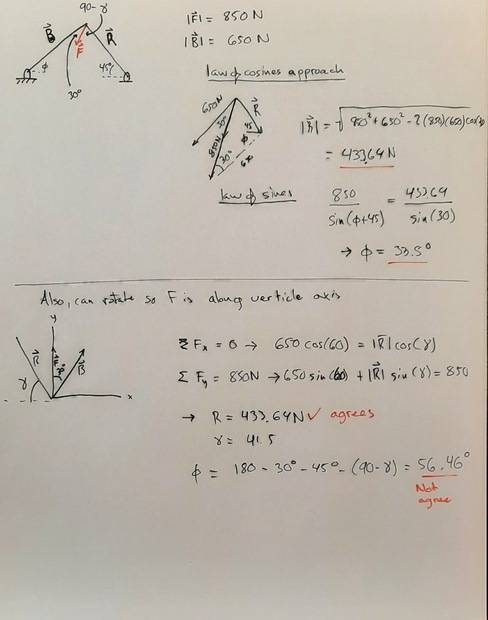
The discussion centers on resolving discrepancies in angle calculations using two methods to find the magnitude and angle of a vector problem involving the sine and cosine rules. The first method, which applied the sine rule, resulted in ambiguous angle solutions, while the second method utilized the cosine rule, providing a definitive angle. The consensus is that the cosine rule is more reliable in this context, as it eliminates ambiguity by allowing for the determination of both magnitude and sign of the angle. The participants emphasize the importance of recognizing the limitations of the sine rule in certain scenarios.
PREREQUISITES
- Understanding of trigonometric functions, specifically sine and cosine.
- Familiarity with the law of sines and the law of cosines.
- Basic knowledge of vector resolution and triangle properties.
- Ability to interpret geometric diagrams related to trigonometric problems.
NEXT STEPS
- Study the law of cosines in detail to understand its applications in vector problems.
- Learn how to resolve vector components using both sine and cosine rules effectively.
- Explore examples of ambiguous solutions in trigonometry and how to address them.
- Practice solving vector problems that require both magnitude and angle determination.
USEFUL FOR
Students and professionals in physics, engineering, and mathematics who are dealing with vector analysis and trigonometric calculations. This discussion is particularly beneficial for those seeking to clarify the application of sine and cosine rules in problem-solving.