Two-bulb experiment for measuring gas diffusivity

[MexChemE]

Hi, PF! I recently solved a problem from BSL which asked to analyze the following system used for determining the diffusivity of a binary mixture of gases.

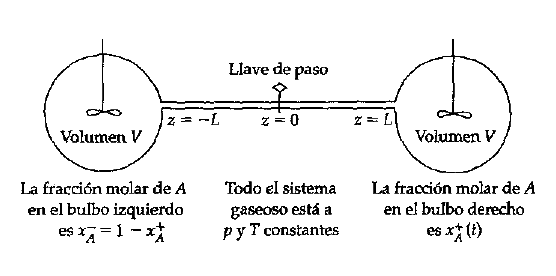
The left portion of the system, from the left bulb up to the stopcock at the middle of the tube, is filled with gas A. The right portion of the system is filled with gas B. At t = 0, the stopcock is opened a the gases start to diffuse. This is a quasi-steady state process. First we derive an expression for the molar flux of A through the tube using a steady state molar balance, and then we make an unsteady state molar balance for species A on the left bulb. The goal is to obtain an expression for x_A^+ as a function of time. The function is
\ln \left(\frac{\tfrac{1}{2} - x_A^+}{\tfrac{1}{2}} \right) = - \frac{SD_{AB} t}{LV}
Where S is the cross-section area of the tube. What got my attention is that the last part of the problem asked to suggest a method of plotting the experimental data in order to find the diffusivity. What I suggested was to define
y = \ln \left(\frac{\tfrac{1}{2} - x_A^+}{\tfrac{1}{2}} \right)
m = - \frac{SD_{AB}}{LV}
Then we can make a linear regression with the data from the experiment and find the slope, then obtain D_{AB} from it.

My actual doubt lies within the implementation of the experiment. Specifically, calculating the mole fraction of gas A in the mixture. Is there a way to do that without using advanced equipment? I.e. can you calculate the mole fraction of A in the mixture using only basic lab equipment?

Thanks in advance for any input!

 

[Chestermiller]

The question is, "how do you measure the mole fraction of a species in a gas sample?" It depends on the situation. If it's water vapor in air, for example, you just condense out the water vapor. In other situations, it might be much more difficult.

Chet

 

[MexChemE]

The question is, "how do you measure the mole fraction of a species in a gas sample?"

Yes, that sounds better. I thought it would be a nice experiment to do at home or school, but measuring mole fractions would be a big problem without the use of sophisticated techniques or equipment.

Here's another question, probably a big misconception though. If I fill one half of the system with oxygen, and the other half with nitrogen, will the steady state concentrations of each species be the same as in air after carrying out the experiment?

Edit: Another related question, if not the same. Do the concentrations of O₂ and N₂ in air depend only on the diffusivity of the O₂-N₂ pair or do they depend on other factors also?

 

[Chestermiller]

Yes, that sounds better. I thought it would be a nice experiment to do at home or school, but measuring mole fractions would be a big problem without the use of sophisticated techniques or equipment.

Here's another question, probably a big misconception though. If I fill one half of the system with oxygen, and the other half with nitrogen, will the steady state concentrations of each species be the same as in air after carrying out the experiment?

What are your thoughts on this?

Edit: Another related question, if not the same. Do the concentrations of O₂ and N₂ in air depend only on the diffusivity of the O₂-N₂ pair or do they depend on other factors also?

What are your thoughts on this?

 

[MexChemE]

What are your thoughts on this?

Well, for the first question, in order for the system to be at constant temperature and pressure, there must be the same amount of moles of each gas in each half of the system. So I guess no, the mole fraction of both oxygen and nitrogen will be 0.5 when the system reaches steady state. This is also what the obtained model tells us. So, in this case, diffusivity affects how fast diffusion will happen, but not the extent of mixing. Therefore, if we want the final mixture to be like air, we should fill one half with 0.21 moles of oxygen and the other half with 0.79 moles of nitrogen, or a proportional multiple of these quantities.

For the second question, I guess diffusivity again plays an insignificant role in the nature of the concentration distribution of air, so it depends in other factors like temperature, pressure and the inherent properties of each gas.

Bottom line: Diffusivity is an important parameter in transport processes/phenomena, but not so useful or significant in equilibrium thermodynamics, right?

 

[Chestermiller]

Well, for the first question, in order for the system to be at constant temperature and pressure, there must be the same amount of moles of each gas in each half of the system. So I guess no, the mole fraction of both oxygen and nitrogen will be 0.5 when the system reaches steady state. This is also what the obtained model tells us. So, in this case, diffusivity affects how fast diffusion will happen, but not the extent of mixing. Therefore, if we want the final mixture to be like air, we should fill one half with 0.21 moles of oxygen and the other half with 0.79 moles of nitrogen, or a proportional multiple of these quantities.

For the second question, I guess diffusivity again plays an insignificant role in the nature of the concentration distribution of air, so it depends in other factors like temperature, pressure and the inherent properties of each gas.

Mainly, the naturally occurring amounts of the gases.

Bottom line: Diffusivity is an important parameter in transport processes/phenomena, but not so useful or significant in equilibrium thermodynamics, right?

Of course not. It's only a transport parameter, and doesn't figure in equilibrium thermodynamics in any way.

Chet