Burning carbon particle -- Boundary conditions

[MexChemE]

I want to model the diffusion-controlled combustion of a small carbon particle. The system I want to model is similar to this one

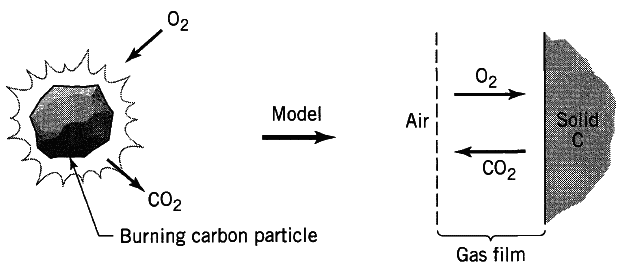
However, I'm not going to use the stagnant gas film model as shown in the figure, since I lack data for the film thickness, and I want to evaluate the problem numerically. Instead, I'm going to use spherical coordinates with boundaries r = R, the radius of the carbon particle, and r = ∞. I'm going to assign A to O₂ and B to CO₂ for the mathematical models. I will be using molar fractions because the global molar density of the system can be considered to be constant. The diffusion equation, concentration profile and molar flux in terms of A are given by
\frac{d}{dr} \left( r^2 \frac{dx_A}{dr} \right) = 0
x_A = x_{A \infty} \left( 1 - \frac{R}{r} \right)
N_{Ar} = - \frac{c \ D_{AB} \ x_{A \infty} R}{r^2}
Where x_A∞ is the molar fraction of oxygen at r = ∞. The negative sign in the molar flux expression is there because oxygen is diffusing towards the carbon particle. My problem lies within giving a numerical value to x_A∞. The statement says the particle burns in presence of air, so first I let x_A∞ = 0.21, but that creates a problem. For this scenario, N_{Ar} = - N_{Br}, and if I make the analysis in terms of B, I obtain the following expressions
x_B = x_{BR} \frac{R}{r}
N_{Br} = \frac{c \ D_{AB} \ x_{BR} R}{r^2}
The problem is that x_BR, the molar fraction of CO₂ in the surface of the carbon particle, is always 1. Then I'm forced to assign x_A∞ = 1, in order for N_{Ar} = - N_{Br} to be satisfied. The problem is that the particle is burning in air, not oxygen, so what about the presence of nitrogen? Do we just consider species A and B and neglect any other species present in the system? Do we ignore nitrogen because it is not participating in the mass transfer process? The process is diffusion-controlled, so I ignored the kinetics of the combustion and setted x_A |_{r=R} = 0 and x_{BR} = x_B |_{r=R} = 1.

My ultimate goal is to calculate the time it takes for the carbon particle to consume completely, using a quasi-steady state analysis. I have enough data to calculate this, but I want to sort this boundary condition issue out first.

The data I have are:
Carbon particle diameter: 0.05 in
Carbon particle density: 85 lb ft^-3
Pressure: 1 atm
Temperature: 2500 °F
Diffusivity: 8 ft² hr^-1

Thanks in advance for any input!

 

[Chestermiller]

I don't see why you are saying that the mole fraction of B at the particle has to be 1. What about the nitrogen in the air at the interface? Where is the diffusion coefficient in your radial diffusion equation? The boundary condition at the particle should be that the flux of B is minus the flux of A. And B has a different diffusion coefficient than A.

Chet

 

[MexChemE]

I don't see why you are saying that the mole fraction of B at the particle has to be 1. What about the nitrogen in the air at the interface?

Well, it hadn't occurred to me to consider the nitrogen presence in the boundary at the particle. If I take into account the nitrogen in the whole system I guess I could say x_BR = x_A∞ = 0.21.

Where is the diffusion coefficient in your radial diffusion equation? (...) And B has a different diffusion coefficient than A.

The diffusivity of the A-B pair is given as a constant datum, so I took it out of the equation, along with c, the molar density of the system, also a constant because we were told to consider constant T and P. Isn't D_AB = D_BA?

The boundary condition at the particle should be that the flux of B is minus the flux of A.

Whenever there's an heterogeneous reaction at a surface, the boundary condition for the molar flux at said surface according to BSL is N_{Ar} |_{r=R} = k_1'' c x_A |_{r=R}. So, in this scenario x_A |_{r=R} = \frac{N_{Ar} |_{r=R}}{k_1'' c} = 0, because the reaction is said to be instantaneous and k_1'' \rightarrow \infty. And then I get x_B from x_B = 1 - x_A.

 

[Chestermiller]

Well, it hadn't occurred to me to consider the nitrogen presence in the boundary at the particle. If I take into account the nitrogen in the whole system I guess I could say x_BR = x_A∞ = 0.21.

The diffusivity of the A-B pair is given as a constant datum, so I took it out of the equation, along with c, the molar density of the system, also a constant because we were told to consider constant T and P. Isn't D_AB = D_BA?

Both A and B are diffusing through nitrogen. So the diffusion coefficients are not the same.

Whenever there's an heterogeneous reaction at a surface, the boundary condition for the molar flux at said surface according to BSL is N_{Ar} |_{r=R} = k_1'' c x_A |_{r=R}. So, in this scenario x_A |_{r=R} = \frac{N_{Ar} |_{r=R}}{k_1'' c} = 0, because the reaction is said to be instantaneous and k_1'' \rightarrow \infty. And then I get x_B from x_B = 1 - x_A.

No. The diffusion coefficients of O2 and CO2 are different. The flux of O2 coming into the surface is the same as the flux of CO2 leaving the surface. The concentration of CO2 at infinity is zero.

Chet

 

[MexChemE]

Both A and B are diffusing through nitrogen. So the diffusion coefficients are not the same.

Oh, I think I got your point now. The statement indeed calls the given diffusivity datum the "diffusivity of oxygen through the mixture."

The flux of O2 coming into the surface is the same as the flux of CO2 leaving the surface.

With this information I can proceed to solve for the time required for the carbon to consume completely. With the boundary condition you provided me with, I can calculate the molar flux of CO₂. This quantity times the surface area of the particle is the molar flow rate of CO₂, which will be used in the quasi-steady state analysis
N_{Br} |_{r=R} = - N_{Ar} |_{r=R} = \frac{c_a \ D_{AC} \ x_{A \infty}}{R}
W_{Br} = 4\pi R^2 N_{Br} |_{r=R} = 4\pi c_a \ D_{AC} \ x_{A \infty} R
I changed the subindex for the diffusivity, C stands for N₂ now, and c_a is the molar density of air. A distinction is made because we will also have the molar density of the carbon particle in the equations. Now, we make an unsteady state mass balance on the carbon particle
\frac{dM}{dt} = - W_{Br}
Where M is the mass of the carbon particle. We can say M= \frac{4}{3} \pi R^3 c_c. Where c_c is the molar density of the carbon particle. The differential equation becomes
R \ c_c \frac{dR}{dt} = c_a \ D_{AC} \ x_{A \infty}
Integrating
\int_0^t dt = - \frac{c_c}{c_a \ D_{AC} \ x_{A \infty}} \int_R^0 R \ dR
t= \frac{c_c R^2}{2 c_a D_{AC} \ x_{A \infty}}
Now some number crunching
c_c = \frac{85 \ \frac{lb}{ft^3}}{12 \ \frac{lb}{lbmol}} = 7.083 \ \frac{lbmol}{ft^3}
c_a = \frac{1 \ atm}{\left(0.7302 \ \frac{atm \cdot ft^3}{lbmol \cdot R}\right)(2960 \ R)} = 4.6266 \times 10^{-4} \frac{lbmol}{ft^3}
R = 0.025 \ in \left( \frac{1 \ ft}{12 \ in} \right) = \frac{1}{480} \ ft
Plugging in the values in the expression for time we finally get
t = 0.0198 \ hr = 1.188 \ min
Which is the time it takes for the small particle to burn completely.

 

[Chestermiller]

Yes. I think that this is correct.

 

[MexChemE]

Thank you! Just one more question, if D_AC ≠ D_BC, is it still safe to assume N_Ar = -N_Br?

 

[Chestermiller]

Thank you! Just one more question, if D_AC ≠ D_BC, is it still safe to assume N_Ar = -N_Br?

For every mole of oxygen that reaches the particle surface, one mole of CO2 leaves.

 

[MexChemE]

So, the relationship which must be satisfied is x_{A \infty} D_{AC} = x_{BR} D_{BC}, where both molar fractions cannot be equal because that would make the diffusivities equal.

If I'd want to estimate the diffusivity of CO₂ in C, should C be N₂ or air?

 

[Chestermiller]

So, the relationship which must be satisfied is x_{A \infty} D_{AC} = x_{BR} D_{BC}, where both molar fractions cannot be equal because that would make the diffusivities equal.

Right

If I'd want to estimate the diffusivity of CO₂ in C, should C be N₂ or air?

I would have to go back an look up the appropriate sections of BSL to answer this one. To a good first approximation, I would use N2. But, the CO2 is also diffusing relative to O2, and the O2 mole fraction is not constant.

 

[MexChemE]

Thanks! I'm going to try with both, and I will also estimate the diffusivity of O₂ in both nitrogen and air for the given conditions and see which one approaches more the value of the given diffusivity.