Dante Tufano
- 32
- 0
So I'm on my last try for this question, and I could really use some help, I'm completely clueless..
Two waves of light in air, of wavelength λ = 460.0 nm, are initially in phase. They then travel through plastic layers as shown in Figure 35-36, with L1 = 4.00 µm, L2 = 3.50 µm, n1 = 1.20, and n2 = 1.60.
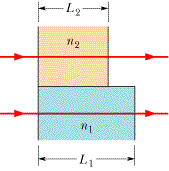
(a) What is their phase difference in cycles after they both have emerged from the layers and arrived at the same horizontal position?
_______________cycles
(b) If the waves at that later position are brought together to a single point, what type of interference occurs?
-closer to destructive interference
-cannot tell from the information given
-closer to constructive interference
2. I know that the change in phase is equal to (L/wavelength)(n-1)
3. I plugged in the given values, and got a phase shift of 4.565 radians for n2 and a shift of 1.739 radians for n1. These added to a shift of 6.304 radians. Since only the decimal matters, it's a shift of .304 radians. However, this is way off, since when I divide by 460nm to get the answer in terms of cycles, I get 661.63, which is wayyyy too large. Even then, I'm clueless on how to answer part b too. Can I please get some help?
Two waves of light in air, of wavelength λ = 460.0 nm, are initially in phase. They then travel through plastic layers as shown in Figure 35-36, with L1 = 4.00 µm, L2 = 3.50 µm, n1 = 1.20, and n2 = 1.60.
(a) What is their phase difference in cycles after they both have emerged from the layers and arrived at the same horizontal position?
_______________cycles
(b) If the waves at that later position are brought together to a single point, what type of interference occurs?
-closer to destructive interference
-cannot tell from the information given
-closer to constructive interference
2. I know that the change in phase is equal to (L/wavelength)(n-1)
3. I plugged in the given values, and got a phase shift of 4.565 radians for n2 and a shift of 1.739 radians for n1. These added to a shift of 6.304 radians. Since only the decimal matters, it's a shift of .304 radians. However, this is way off, since when I divide by 460nm to get the answer in terms of cycles, I get 661.63, which is wayyyy too large. Even then, I'm clueless on how to answer part b too. Can I please get some help?