PFuser1232
- 479
- 20
Homework Statement
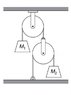
Masses ##M_1## and ##M_2## are connected to a system of strings and pulleys as shown (I have attached an image). The strings are massless and inextensible, and the pulleys are massless and frictionless. Find the acceleration of ##M_1##.
Homework Equations
$$\sum_{}^{} F_y = m \ddot{y}$$
The Attempt at a Solution
[/B]
I think I got the right answer, but I want to know if my reasoning is correct. Now, both strings are massless, so the tension has to be the same throughout (for both strings). If the tension acting on ##M_1## is ##T##, so is the tension acting on the second pulley. The second pulley does not accelerate, therefore the net force on the second pulley must be zero, and so the tension on each side (pulling the pulley down) must be ##\frac{1}{2} T##. ##M_2## is in equilibrium, giving us the equation:
$$\frac{1}{2} T = M_2 g$$
$$T = 2 M_2 g$$
Now, applying Newton's second law to ##M_1##:
$$T - M_1 g = M_1 \ddot{y}$$
$$2M_2 g - M_1 g = M_1 \ddot{y}$$
$$\ddot{y} = \frac{g(2M_2 - M_1)}{M_1}$$
I have two questions:
1) Why exactly is the net force on the second pulley zero? Is it because the setup makes it impossible for the pulley to accelerate? Or is it because its mass is negligible?
2) The equation for acceleration tells us that if ##2M_2 > M_1##, ##M_1## will accelerate upwards. If ##2M_2 < M_1##, ##M_1## will accelerate downwards. If ##M_1 = 2M_2##, ##M_1## does not accelerate. If ##M_1## accelerates while the string is taut, doesn't this mean the second pulley should accelerate? And if the second pulley accelerates, doesn't this mean ##M_2## should accelerate? This contradicts my first equation, ##T = 2 M_2 g##.