Two people on a boat(center of mass)

[Toranc3]

Homework Statement

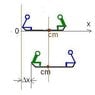
Two people, one of mass 75kg and the other of mass 60kg, sit in a rowboat of mass 80kg. With the boat initially at rest, the two people, who have been sitting at opposite ends of the boat, 3.2m apart from each other, exchange seats.
How far will the boat move?
and in what direction will the boat move?

Homework Equations

xcm=x1m1+x2m2+xbmb/(m1+m2+mb)

The Attempt at a Solution

m1=75kg person initially on left end of boat.
m2=60kg person initially on right end of boat.
mb=80kg boat

my origin is at the left end of the boat and the 75kg person is initially there.

xcm=x1m1+x2m2+xbmb/(m1+m2+mb)

xcm=(0)(75kg) + (3.2)(60kg) + (1.6)(80kg)/(75kg+60kg+80kg)

xcm= 1.4883mNow for my final(center of mass doesn't move)

1.4883m=x1m1+ x2m2 +xbmb/(m1+m2+mb)

1.4883m= (3.2m)(75kg) + (0)(60kg) + xb(80kg)/(215kg)

xb(final) = 1.004375m

xb(final)-xb(initial)

1.004375m- 1.4883m=-.4839m

Is this correct? Thanks!

 

[Sunil Simha]

my origin is at the left end of the boat and the 75kg person is initially there.

xcm=x1m1+x2m2+xbmb/(m1+m2+mb)

xcm=(0)(75kg) + (3.2)(60kg) + (1.6)(80kg)/(75kg+60kg+80kg)

xcm= 1.4883m

This calculation is correct.

Now for my final(center of mass doesn't move)

1.4883m=x1m1+ x2m2 +xbmb/(m1+m2+mb)

1.4883m= (3.2m)(75kg) + (0)(60kg) + xb(80kg)/(215kg)

xb(final) = 1.004375m

xb(final)-xb(initial)

1.004375m- 1.4883m=-.4839m

Here you are committing a mistake. You are right in saying that the centre of mass doesn't move but in your calculation, you have taken x₁ to be equal to 3.2m. But the boat actually moves (by y metres towards left, say). This would imply x₁ =3.2-y. Similar corrections need to be made for other masses.

 

[haruspex]

Also, there's an easier way. You can think of the swap as equivalent to a transfer of 15kg rightwards by 3.2m. Now you need to compute the distance leftwards the system as a whole has to move to compensate for that.

 

[Toranc3]

Hey I am still stuck. Ok so the center of mass is correct right? Xcm =1.49m

How would I set up my final positions?

1.49(215kg) = (x1f)m1 + (x2f)m2 + (xbf)mb

 

[Toranc3]

I know that I am supposed to get x1f and x2f in terms of xbf and solve for xbf but I am not sure how.

 

[cmkc109]

Also, there's an easier way. You can think of the swap as equivalent to a transfer of 15kg rightwards by 3.2m. Now you need to compute the distance leftwards the system as a whole has to move to compensate for that.

just wondering, does it mean the origin is still at x=0, but then now 75kg is acting at 3.2m, and 80kg at 1.6m ? So wouldn't the center of mass shift since the balance has changed?

 

[Toranc3]

just wondering, does it mean the origin is still at x=0, but then now 75kg is acting at 3.2m, and 80kg at 1.6m ? So wouldn't the center of mass shift since the balance has changed?

I was thinking the same too!

 

[cmkc109]

I was thinking the same too!

The first part is 1.488m

For the second part, I got 1.711m

75 (3.2) + 80 (1.6) /215kg
= 1.711 m

The boat moves 1.711 - 1.488 = 0.223m

I think I get it now,
the center of mass of the boat won't change, so after they switch location, the boat actually moves to compensate that change. It will move to the left according to Newton's third law. Since the person is exerting a forward force, the reaction force will be to the back, causing the boat to move leftwards

 

[Toranc3]

The first part is 1.488m

For the second part, I got 1.711m

75 (3.2) + 80 (1.6) /215kg
= 1.711 m

The boat moves 1.711 - 1.488 = 0.223m

I think I get it now,
the center of mass of the boat won't change, so after they switch location, the boat actually moves to compensate that change.

Yeah that is correct. It moves .223m towards the initial position of the 75kg person. Ok but from our zero, the center of mass moves then? However the distance from the two people to the center of mass remains the same?

 

[Toranc3]

The first part is 1.488m

For the second part, I got 1.711m

75 (3.2) + 80 (1.6) /215kg
= 1.711 m

The boat moves 1.711 - 1.488 = 0.223m

I think I get it now,
the center of mass of the boat won't change, so after they switch location, the boat actually moves to compensate that change. It will move to the left according to Newton's third law. Since the person is exerting a forward force, the reaction force will be to the back, causing the boat to move leftwards

Yo thanks for the help. I think I get it now.

 

[Toranc3]

How would this be done if you were to equate the original center of mass to your final values?

 

[cmkc109]

Yeah that is correct. It moves .223m towards the initial position of the 75kg person. Ok but from our zero, the center of mass moves then? However the distance from the two people to the center of mass remains the same?

The center of mass only change if there is external force applied on the system. But here there is only a change in the balance, but the overall force is the same, so the CoM remains the same. From the calculation, you see we get an answer of 1.7m, but since the CoM remains the same, the system has to move back to 1.7 -1.4 to compensate the change.

How would this be done if you were to equate the original center of mass to your final values?

not sure what are you asking

 

[Toranc3]

The center of mass only change if there is external force applied on the system. But here there is only a change in the balance, but the overall force is the same, so the CoM remains the same. From the calculation, you see we get an answer of 1.7m, but since the CoM remains the same, the system has to move back to 1.7 -1.4 to compensate the change.




not sure what are you asking

Well originally I had this:

Since the center of mass doesn't change(1.49m)

1.49m= (x2f)m2+(x1f)m1+(xbf)mb/(215kg)

x2f=x2 final

Since the center of mass doesn't change couldn't this problem be done this way too? When I had this setup I got stuck.

 

[haruspex]

just wondering, does it mean the origin is still at x=0, but then now 75kg is acting at 3.2m, and 80kg at 1.6m ? So wouldn't the center of mass shift since the balance has changed?

Sorry, I don't understand your question. My method says it's (75-60)*3.2/(75+60+80) = .2233m. 75-60kg moved right 3.2m, so to restore the overall COM the system as a whole, 6+75+80kg, has to move left .2233m.

 

[ehild]

A figure always helps. Let be the origin at the initial right edge of the boat, where the 60 kg man (the blue one) sits. The position of the cm is 1.71 m. When the men change positions, the green one is at Δx and the blue one is at 3.2+ Δx, and the centre of the boat is at 1.6+Δx.The cm stays at the same position: 75Δx + (1.6+Δx)80+(3.2+Δx)60=1.71(75+80+60)

ehild

Edit:If the 75 kg man sits at the left end the boat will move to the left.

 

[TSny]

Lots of ways to think about this problem. Here's a way I like. Suppose you first calculate the location of the cm of the system relative to the center of the boat:

x_c = [(75kg)(-1.6 m) + (60 kg)(+1.6 m) + (80 kg)(0)]/215 kg = -.1116 m.

So, the cm is initially 0.1116 m to the left of the center of the boat.

When the people switch places, clearly the cm will now be 0.1116 m to the right of the center of the boat.

To keep the center of mass from moving relative to the water, how far and in what direction must the boat move?

 

[Toranc3]

Thanks for the help guys. I was originally trying to do ehilds method but going to the left. I got it now and understand it. I will certainly try your method too Tsny. THanks again!