Two rotating masses balanced by a third mass (rotational dynamics)

[Eirik]

Homework Statement:

Hi! This isn't really homework, but I'm practicing for my exam in mechanical physics and I'm really struggling with this one question!

Two masses, m, are rotating around the z axis as shown in the figure on a frictionless surface, but are being pulled down by a third mass, M. Find the differential equation for the movement of the system. The masses should be considered point masses and the system initially has $R=R_0$ and $\omega=\omega_0$ It should be on the following form, where $\alpha$ and $\beta$ are constants you need to find:

Relevant Equations:

$\ddot R + \alpha g - \frac{\beta}{R^3}=0$, differential equation I need to find

$a_r = \ddot R -\omega^2R$, acceleration of mass m in the circle, given in task

Here's a diagram of what the system looks like:

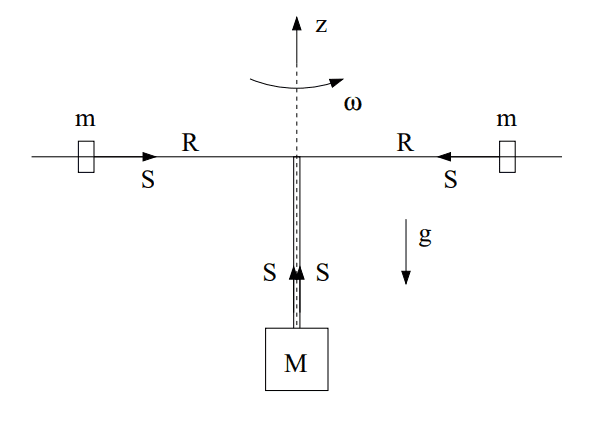
So far I have figured out what the initial angular velocity is, if the system is balanced (no movement):

$\sum F_m = m*\frac{v^2}{R_0}-\frac{Mg}{2}=0$
$m \frac{v^2}{R_0}-\frac{Mg}{2}=0$ divide both sides by m
$\omega_0 = \sqrt{\frac{Mg}{2mR_0}}$

One of the hints given for the task, was that we should consider the conservation of angular momentum:
Moment of inerty, start: $I_0=2mR_0^2$
Angular momentum, start: $L_0=I_0\omega_0=2mR_0^2 \sqrt{\frac{Mg}{2mR_0}}$

I am struggling to find the equation for the angular momentum after that, however. I know that the moment of inertia should still be $I=2mR^2$, and that $L=I\omega$. How do I find \omega?

I also have this:
$\sum F_M = Mg-2S=M*\ddot R$
$S=m* (\ddot R -\omega^2R)$ Really not sure if this one is correct

Any help would be very greatly appreciated!

 

[TSny]

Homework Statement::
So far I have figured out what the initial angular velocity is, if the system is balanced (no movement):

If the system were to start out in the balanced state, then it would remain in this state. I don't think they want you to assume the system is in the balanced state initially. I think they want you to express the differential equation for $\ddot R$ in terms of $R_0$ and $\omega_0$.

One of the hints given for the task, was that we should consider the conservation of angular momentum:
Moment of inerty, start: $I_0=2mR_0^2$
Angular momentum, start: $L_0=I_0\omega_0=2mR_0^2 \sqrt{\frac{Mg}{2mR_0}}$

Since the system does not necessarily start in the balanced state, you cannot assume that $\omega_0=\sqrt{\frac{Mg}{2mR_0}}$. Just express $L_0$ in terms of $m$, $R_0$, and $\omega_0$.

I am struggling to find the equation for the angular momentum after that, however. I know that the moment of inertia should still be $I=2mR^2$, and that $L=I\omega$.

Yes.

How do I find $\omega$?

You can use the expression for the angular momentum to find $\omega$ as a function of $R$.

I also have this:
$\sum F_M = Mg-2S=M*\ddot R$

Be careful with signs. The left side expresses the net downward force on $M$. So, the acceleration on the right should be the downward acceleration of $M$. Does the downward acceleration of $M$ equal $\ddot R$ or $-\ddot R$?

$S=m* (\ddot R -\omega^2R)$

You have a sign error in this equation. Does the force $S$ on $m$ act in the radially outward direction or the radially inward direction?

 

[Eirik]

Thank you so much @TSny ! That was really, really helpful!

Then we have
$L_i=L$
$2mR_0^2\omega_0=2mR^2\omega$
Solving for $\omega$ gives us $\omega=\frac{R_0^2\omega_0}{R^2}$

And if we choose the positive direction for the accelaration along -z, it should be $S=m*(\omega^2R-\ddot R)$ instead, as the direction for m's acceleration will be radially inward. If I now substitute $\omega$ in this expression, I get:

$S=m*((\frac{R_0^2\omega_0}{R^2})^2R-\ddot R) = m(\frac{R_0^4\omega_0^2}{R^3}-\ddot R)$

Substitution in $Mg-2S=M\ddot R$ gives us:

$Mg-2(m(\frac{R_0^4\omega_0^2}{R^3}-\ddot R))=M\ddot R$

And after doing some algebra I get:

$\ddot R - \frac{M}{M-2m}g + \frac{\frac{2mR_0^4\omega_0^2}{M-2m}}{R^3}=0$

Meaning that $\alpha = \frac{M}{M-2m}$ and $\beta = \frac{2mR_0^4\omega_0^2}{M-2m}$

Yay! Does that look right?

 

[TSny]

Everything looks good up to here:

Substitution in $Mg - 2S = M \ddot R$

This equation has a sign error. Review the comments near the end of post #2. This will alter your final result. Otherwise, I think you have it.

 

[Eirik]

@TSny Yes, of course! 🤦‍♂️ I thought $\ddot R$ would be M's downward acceleration, but R will get smaller over time, so it has to be $Mg-2S=-M\ddot R$

That finally gives me

$\ddot R + \frac{M}{M+2m}g - \frac{\frac{2mR_0^4\omega_0^2}{M+2m}}{R^3}=0$

with $\alpha = \frac{M}{M+2m}$ and $\beta = \frac{2mR_0^4\omega_0^2}{M+2m}$

That also checks out with the signs the task said I was supposed to end up with lol

Thank you again so, so much for all the help!