U substitution and integration by parts

[robertjford80]

I would think because of this

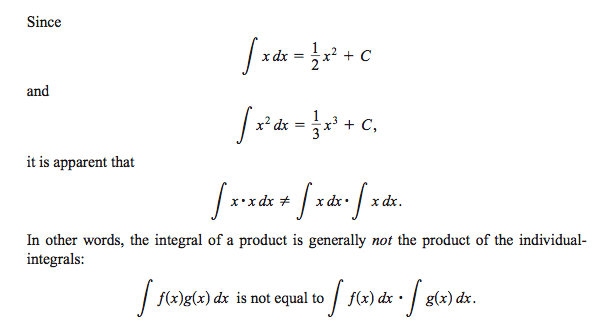
The following problem:

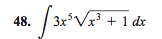
At this stage they should use integration by parts:

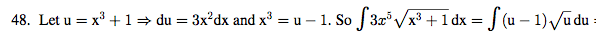
However, maybe integration by parts is only useful when one of the parts is e^x ln or a trigonometric formula.

 

[cjc0117]

Integration by parts can be useful whenever the integrand is a product of two functions. But it is not always the easiest method to use. For instance, the integral $\int(u-1)\sqrt{u}du=\int(u^{3/2}-u^{1/2})du$ can easily be solved using the power rule in reverse. Of course, you could solve it using integration by parts as well, but it's just more work than is necessary.

 

[robertjford80]

good, thanks.

 

[Villyer]

What would be your u and what would be your dv?

Using integration by parts might work, but I feel that even if it does work it will be much more work than using u substitution.Is the problem here that you don't find the u substitution they used to be 'legal'?

 

[robertjford80]

Yea, it doesn't seem legal, because I thought you couldn't take the product of two functions in an integrand.

 

[jgens]

Yea, it doesn't seem legal, because I thought you couldn't take the product of two functions in an integrand.

You need to work on being more precise. The integrand of $\int_0^1 x^2 \mathrm{d}x$ is the product of two functions but is clearly integrable.