mk9898
- 109
- 9
How/why does the first equal sign hold? Where does each derivative come from:
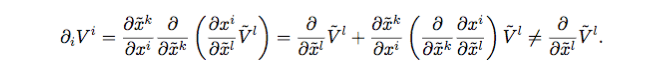
The discussion focuses on the derivation of tensor equations, specifically addressing the application of the chain rule and product rule in tensor calculus. Participants clarify the transformation properties of vector components and the cancellation of derivatives, emphasizing the role of the Kronecker delta in simplifying expressions. The second equal sign in the equations is confirmed correct, highlighting the importance of understanding operator behavior in derivatives. Key insights include the necessity of recognizing the uniqueness of vector component dependence for accurate tensor transformations.
PREREQUISITESMathematicians, physicists, and engineers involved in advanced studies of tensor calculus and those seeking to deepen their understanding of vector transformations and derivative operations.
That is the second term, not the first term...mk9898 said:I'm not seeing how they cancel since they are operators.