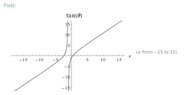
If we rewrite the given equation to make $\tan \theta$ the subject, and then plot a graph of $\tan \theta$ versus $x$, we get:
$\tan \theta=\dfrac{x^2+2x-1}{x+1}$
View attachment 2393
Note:
$x=-1$ is a vertical asymptote
Consider the fact that $x$ are two integrals regardless of what $\tan \theta$ is(i.e. try to imagine we are to move a ruler horizontally on the graph and we have to hit two $x$ of which both are integers), we can deduce that
i. This is impossible for the region where $x<-3$,
ii. This is only possible only when one of the $x$ is in the interval $-3<x<0$.
Therefore
a. when $x=-2$ and this gives $\tan \theta=\dfrac{(-2)^2+2(-2)-1}{(-2)+1}=1$
b. since $x\ne-1$ so we're done.
Hence, the sum of all possible values of $\theta$ in the interval $(0, 2\pi)$ is $\dfrac{\pi}{4}+\dfrac{5\pi}{4}=\dfrac{3\pi}{2}$ and that shows $k=\dfrac{3}{2}$.