Uncovering the Missing Solution in the Modulus Problem: k>4 and k=0

Thread starter chwala
Start date Oct 6, 2021
Tags

Modulus

Oct 6, 2021

chwala

Gold Member

Homework Statement: Find the set of values of ##k## for which ##|(x+5)(x+1)|=k## has two solutions

Relevant Equations: modulus

i got ##k>4## and ##k=0##
find my working...

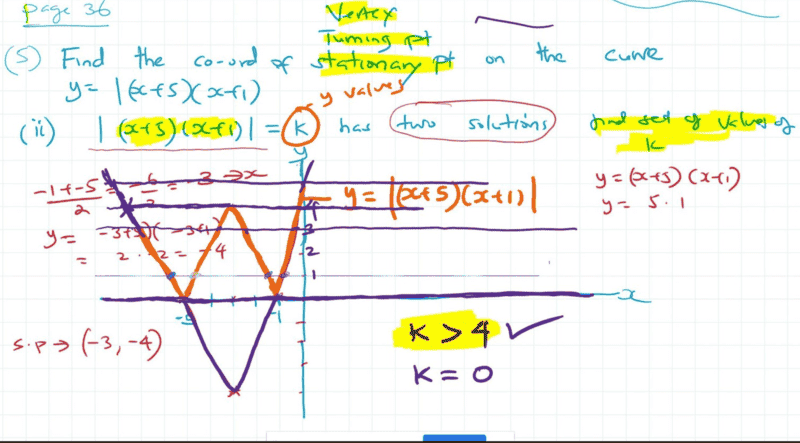
the test book gives solution as ##k>4##. Did they miss out on the second solution ##k=0##?

Physics news on Phys.org

Physicists unlock secrets of stellar alchemy, yielding new insights into gold's cosmic origins
A 'seating chart' for atoms helps locate their positions in materials
Light particles prefer company: Photons exhibit collective behavior only after reaching certain threshold

Oct 7, 2021

anuttarasammyak

Gold Member

k=0 and k>4 are solutions as you say.

Oct 7, 2021

chwala

Gold Member

anuttarasammyak said:

k=0 and k>4 are solutions as you say.

Thanks Man...meaning the author was not keen. Cheers! Bingo

Thread 'Complex Numbers (Laurent Series)'

see attached.

View full post »

Thread 'Necessary criterion for expressing f(a + b)'

It's easy to see that any polynomial is function of that class. Also it seems that composition of exponent and polynomial is good as well. G_f(a, b) should be equal G_f(b, a) as the f(a+b) is symmetrical. Does anyone have information about this or at least related to it?

View full post »

Thread 'Use greedy vertex coloring algorithm to prove the upper bound of χ'

Hi! I am struggling with the exercise I mentioned under "Homework statement". The exercise is about a specific "greedy vertex coloring algorithm". One definition (which matches what my book uses) can be found here: https://people.cs.uchicago.edu/~laci/HANDOUTS/greedycoloring.pdf Here is also a screenshot of the relevant parts of the linked PDF, i.e. the def. of the algorithm: Sadly I don't have much to show as far as a solution attempt goes, as I am stuck on how to proceed. I thought...

View full post »