SUMMARY
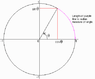
The discussion focuses on the relationship between sinusoidal waves and trigonometric functions, particularly sine and cosine. Participants emphasize that waves exhibit periodicity, which necessitates the use of trigonometric functions to describe their characteristics such as amplitude, phase shift, and frequency. The connection between circular motion and wave behavior is clarified through the unit circle, where sine and cosine represent the coordinates of points on the circle. Understanding these relationships is essential for grasping the mathematical foundations of wave behavior.
PREREQUISITES
- Basic understanding of trigonometric functions (sine, cosine)
- Familiarity with the unit circle and its properties
- Knowledge of wave characteristics (amplitude, frequency, phase shift)
- Intermediate Algebra skills for studying Trigonometry
NEXT STEPS
- Study the unit circle and its relationship to trigonometric functions
- Learn about wave properties and their mathematical descriptions
- Explore graphical representations of sine and cosine functions
- Investigate the concept of angular velocity and its impact on waveforms
USEFUL FOR
Students of mathematics, physics enthusiasts, and anyone seeking to understand the mathematical principles underlying sinusoidal waves and trigonometry.