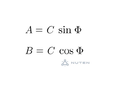Don’t understand the general form of the Sinusoidal Wave Equation

[jjson775]

TL;DR Summary

Don’t understand the general form of the sinusoidal wave equation.

I am a retired engineer, 81 years old, self studying modern physics using Young and Freedman University Physics.

I am familiar with the wave equation y(x,t) = A cos (kx - wt) where A = amplitude, k = wave number and w (omega) = angular frequency.

in the chapter introducing quantum mechanics, this equation is shown as:
y(x,t) = A cos (kx - wt) + B sin (kx - wt). What is the “B” part? Is it another amplitude? The equation is not shown in this form at all in the chapter on mechanical waves.

 

[Ibix]

Are you familiar with the trigonometric identity $C\sin(\theta+\phi)=C\sin(\theta)\cos(\phi)+C\cos(\theta)\sin(\phi)$? If you replace $\theta$ with $kx-\omega t$ can you see what $A$ and $B$ are?

By the way, if you're going to post maths here it's worth having a read of the LaTeX Guide, linked below the reply box. It makes maths much easier to read. There's a known bug that the maths doesn't render in preview, so you may possibly need to refresh the page to see the maths - if you see # marks in my previous paragraph, you need to refresh.

 

[jjson775]

I still don’t see where this is headed.

 

[Ibix]

That's all there is to it.

The point is that with $C\sin(kx+\omega t)$, at $t=0$ the amplitude at $x=0$ is always zero. But that isn't always what you want. Sometimes the amplitude is non-zero at $x=0$ and zero at some other point, which is to say that there is an offset in your wave, usually denoted $\phi$. The equation of that wave is $C\sin(kx+\omega t+\phi)$. You can get to the expression you asked about with the trigonometric identity I quoted.

What you have here is an example of decomposing a wave into two waves added together. The trigonometric identity shows you that a wave with some arbitrary phase offset can be written as a sine wave with a certain amplitude and no phase offset plus a cosine wave with a certain amplitude and no phase offset. It's purely a mathematical trick, but sometimes makes subsequent maths easier.

So the answer to your question is that $A$ and $B$ are the amplitudes of the sine and cosine waves with zero phase offset that you need to add together to get a single sine wave of amplitude $C$ and phase offset $\phi$. You've worked out the mathematical relationships between $A$, $B$ and $C$.

 

[jjson775]

Got it. Thanks! I have seen this equation pop up in lectures on YouTube and now in my textbook without any derivation or explanation. A useful mathematical trick, as you say.

 

[jjson775]

Your comment that it can make subsequent math easier is spot on. It showed up in my textbook to show how it satisfies the general wave equation using partial differentiation leading up to introduction of the Schrödinger equation.