fab13
- 300
- 7
Hello,
I try to apprehend the notion of covariant derivative. In order to undertsand better, here is a figure on which we are searching for express the difference \vec{V} = \vec{V}(M') - \vec{V}(M) :
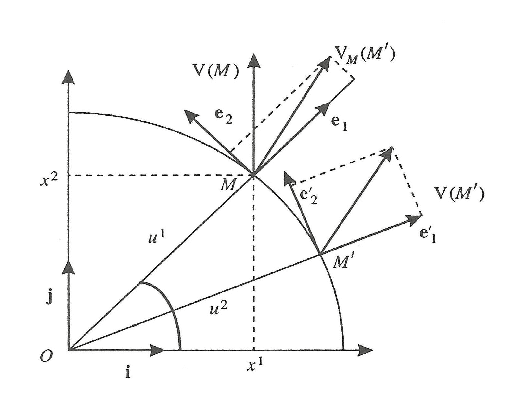
In order to evaluate this difference, we do a parallel transport of \vec{V}(M') at point M.
When one writes what we call "the absolute differential" \text{D}\,v_{k} :
\text{D}\,v_{k} = (\partial_{j}\,v_{k} - v_{i}\Gamma_{jk}^{i})\,dy^{j}
does \text{D}\,v_{k} represent the difference that we could get if the 2 vectors \vec{V}(M') and \vec{V}(M) were expressed in the Cartesian referential ?
So that we could write also from the above figure (with \theta=\theta(M) :
\text{D}\,v_{x}=(\vec{V}_{\rho}(M')-\vec{V}_{\rho}(M))cos(\theta)
and
\text{D}\,v_{y}=(\vec{V}_{\rho}(M')-\vec{V}_{\rho}(M))sin(\theta)
??
Then, if this covariant derivative is zero, one can write :
\text{d}\,v_{k} = v_{j}\,\Gamma_{ik}^{j}\,dy^{i}
does it significate curvilinear coordinates changes in the way that they are equal to v_{j}\,\Gamma_{ik}^{j}\,dy^{i} ?
In the case of a parallel transport of vector \vec{V}(M') from M' point to M point, why absolute differential between the
two vectors is equal to zero whereas the two vectors are not equal in the Cartesian coordinates system (O,x,y) ?
And if I take the same curvilinear coordinates for the two vectors, I get for the absolute differential :
\text{D}\,v_{k} = v_{j}\,\Gamma_{ik}^{j}\,dy^{i}
What does this case represent on the above figure ?
If anyone could help me to clarify this notion of covariant derivative and parallel transport.
Thanks.
I try to apprehend the notion of covariant derivative. In order to undertsand better, here is a figure on which we are searching for express the difference \vec{V} = \vec{V}(M') - \vec{V}(M) :
In order to evaluate this difference, we do a parallel transport of \vec{V}(M') at point M.
When one writes what we call "the absolute differential" \text{D}\,v_{k} :
\text{D}\,v_{k} = (\partial_{j}\,v_{k} - v_{i}\Gamma_{jk}^{i})\,dy^{j}
does \text{D}\,v_{k} represent the difference that we could get if the 2 vectors \vec{V}(M') and \vec{V}(M) were expressed in the Cartesian referential ?
So that we could write also from the above figure (with \theta=\theta(M) :
\text{D}\,v_{x}=(\vec{V}_{\rho}(M')-\vec{V}_{\rho}(M))cos(\theta)
and
\text{D}\,v_{y}=(\vec{V}_{\rho}(M')-\vec{V}_{\rho}(M))sin(\theta)
??
Then, if this covariant derivative is zero, one can write :
\text{d}\,v_{k} = v_{j}\,\Gamma_{ik}^{j}\,dy^{i}
does it significate curvilinear coordinates changes in the way that they are equal to v_{j}\,\Gamma_{ik}^{j}\,dy^{i} ?
In the case of a parallel transport of vector \vec{V}(M') from M' point to M point, why absolute differential between the
two vectors is equal to zero whereas the two vectors are not equal in the Cartesian coordinates system (O,x,y) ?
And if I take the same curvilinear coordinates for the two vectors, I get for the absolute differential :
\text{D}\,v_{k} = v_{j}\,\Gamma_{ik}^{j}\,dy^{i}
What does this case represent on the above figure ?
If anyone could help me to clarify this notion of covariant derivative and parallel transport.
Thanks.