- #1
fab13
- 312
- 6
1) Firstly, in the context of a dot product with Einstein notation :
$$\text{d}(\vec{V}\cdot\vec{n} )=\text{d}(v_{i}\dfrac{\text{d}y^{i}}{\text{d}s})$$
with ##\vec{n}## representing the cosine directions vectors, ##v_{i}## the covariant components of ##\vec{V}## vector, ##y^{i}## the curvilinear coordinates and ##s## an affine parameter (it may be the length along the line, isn't it ?)
Author says that ##\dfrac{\text{d}y^{i}}{\text{d}s}## (with ##y^{i}## curvilinear coordinates) represent the cosine directions and I would like to prove it : how to do it ?
For example, in polar coordinates, How can I express the 2 cosine directions with the 2 vectors curvilinear basis ##\vec{e_{r}}## and ##\vec{e_{\theta}}## ?
On the following figure, I don't know exactly how to represent the vector ##\vec{n}## :
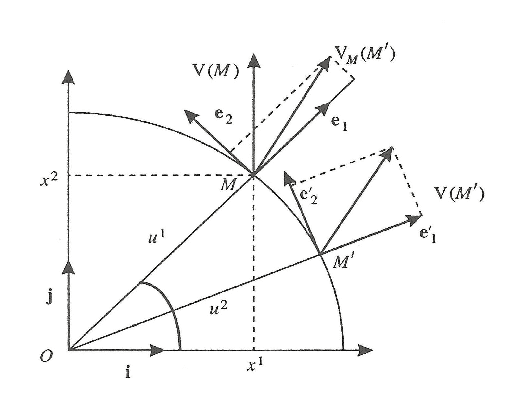
2) Secondly, if ##\dfrac{\text{d}y^{i}}{\text{d}s}## are cosine directions, why does above scalar product is not equal rather to :
$$\text{d}(\vec{V}\cdot\vec{n} )=\text{d}(v^{i}\dfrac{\text{d}y^{i}}{\text{d}s})$$
with ##v^{i}## the contravariant components of ##\vec{V}##. ?
Indeed,both (##v_{i}## and ##v^{i}##) are related by :
$$v_{i}=v^{i}\,\cos(\theta_i)$$ with ##\cos(\theta_i)## the cosine direction for the angle ##\theta_i## between ##\vec{V}## and ##\vec{n}## vectors.
I hope you will understand these 2 questions.
Any help is welcome, Thanks
$$\text{d}(\vec{V}\cdot\vec{n} )=\text{d}(v_{i}\dfrac{\text{d}y^{i}}{\text{d}s})$$
with ##\vec{n}## representing the cosine directions vectors, ##v_{i}## the covariant components of ##\vec{V}## vector, ##y^{i}## the curvilinear coordinates and ##s## an affine parameter (it may be the length along the line, isn't it ?)
Author says that ##\dfrac{\text{d}y^{i}}{\text{d}s}## (with ##y^{i}## curvilinear coordinates) represent the cosine directions and I would like to prove it : how to do it ?
For example, in polar coordinates, How can I express the 2 cosine directions with the 2 vectors curvilinear basis ##\vec{e_{r}}## and ##\vec{e_{\theta}}## ?
On the following figure, I don't know exactly how to represent the vector ##\vec{n}## :
2) Secondly, if ##\dfrac{\text{d}y^{i}}{\text{d}s}## are cosine directions, why does above scalar product is not equal rather to :
$$\text{d}(\vec{V}\cdot\vec{n} )=\text{d}(v^{i}\dfrac{\text{d}y^{i}}{\text{d}s})$$
with ##v^{i}## the contravariant components of ##\vec{V}##. ?
Indeed,both (##v_{i}## and ##v^{i}##) are related by :
$$v_{i}=v^{i}\,\cos(\theta_i)$$ with ##\cos(\theta_i)## the cosine direction for the angle ##\theta_i## between ##\vec{V}## and ##\vec{n}## vectors.
I hope you will understand these 2 questions.
Any help is welcome, Thanks

