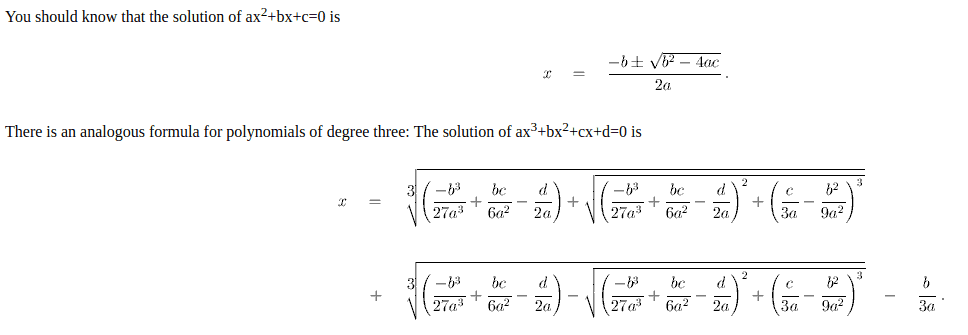Let $ax^3+bx^2+cx+d=0$ where $a\neq0$ and $a,b,c,d$ are arbitrary real numbers. Divide $a$ through the previous equation (since the roots of the previous equation does not change if it is modified by the division): $$x^3+b'x^2+c'x+d'=0 \, \text{where} \, b'=\frac{b}{a}, c'=\frac{c}{a}, \text{and}\,\, d'=\frac{d}{a} \, \text{(1).}$$ By introduction of a new unknown this equation can be simplified, moreover, so that (1) will not have a second power of the unknown. To do what I have described I need to set $x=y+k$ with $k$ still arbitrary. By Taylor's formula (look up in a calculus textbook if you don't know), I will use the first four terms of the formula to determine what the value of $k$: So let $f(x)=x^3+b'x^2+c'x+d'$. $f(y+k)=f(k)+f'(k)y+\frac{f''(k)}{2}y^2+\frac{f'''(k)}{6}y^3$ and $f(k)=k^3+b'k^2+c'k+d'$, $f'(k)=3k^2+2b'k+c'$, $\frac{1}{2}f''(k)=3k+b'$, $\frac{1}{6} f'''(k)=1$. To get rid of the term involving $y^2$, it is suffices to choose $k$ so that $3k+b'=0 \implies k=\frac{-b'}{3}$. We will plugin the value of $k$ into the following functions $f$ and $f'$ and it yields the following values:
$$f\left(\frac{-b'}{3}\right)=d'-\frac{b'c'}{3}+\frac{2{b'}^2}{27} \, \, \text{and} \, \, f'\left(\frac{-b'}{3}\right)=c'-\frac{{b'}^2}{3}.$$ So the substitution for the elimination of $y^2$ is $x=y-\frac{b'}{3}.$ Then the equation (1) is transformed into the following equation through the substitution: $$y^3+py+q=0\, \text{(2)} \, \text{where} \, \, p=c'-\frac{{b'}^2}{3} \, \text{and} \, q= d'-\frac{b'c'}{3}+\frac{2{b'}^2}{27}.$$ A cubic equation of the form (2) can be solved by means of the following device: We seek to satisfy it by setting $y=u+v$, thus introducing two variables $u$ and $v$. On substituting this expression into (2) and arranging terms in a proper way, $u$ and $v$ have to satisfy the equation (let's called it (3): $$u^3+v^3+(p+3uv)(u+v)+q=0,$$ with two variables. This problem is indeterminate unless we find another relationship between $u$ and $v$. This is the relationship that we will be using $3uv+p=0 \implies uv=\frac{-p}{3}$. Then, it follows from (3) that $u^3+v^3=-q$, so that the solution of the cubic (2) can be obtained by solving the system of two equation:$$\begin{cases} u^3+v^3=-q \\ uv=\frac{-p}{3} \end{cases}$$ Taking the cube to the second equation, we will have $u^3v^3=\frac{-p^3}{27}$ and so, from the system of equations and the previous equation, we know the sum and product of the two unknown quantities $u^3$ and $v^3$. (How? There is a formula called the Viete's formula that describes how the roots of a polynomial is related to the coefficient of the same polynomial). These quantities are the roots of the quadratic equation: $t^2+qt-\frac{p^3}{27}=0$. We will separate the roots of the quadratic into $A$ and $B$, respectively: $$A=-\frac{q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}} \,\text{and}\, B=-\frac{q}{2}-\sqrt{\frac{q^2}{4}+\frac{p^3}{27}} $$ where we at liberty to the square root as we please. Now owing to the symmetry between the terms $u^3$ and $v^3$ in the systems of equation, we can set $u^3=A$ and $v^3=B$. If some determined value of the cube root of $A$ is denoted $\sqrt[3]{A}$, the three possible values of $u$ will be $u=\sqrt[3]{A}$, $u=\omega\sqrt[3]{A}$, $u={\omega}^2\sqrt[3]{A}$, where $\omega=\frac{-1+i\sqrt{3}}{2}$ is an imaginary cube root of unity. As to $v$, it will have also three values: $v=\sqrt[3]{B}$, $v=\omega\sqrt[3]{B}$, $v={\omega}^2\sqrt[3]{A}$ but not every one of them can be associated with three possible values of $u$, since $u$ and $v$ must satisfy the relation $uv=-\frac{p}{3}$. If $\sqrt[3]{B}$ stands for that cube root of $B$ which satisfies the relation $\sqrt[3]{A}\sqrt[3]{B}=-\frac{p}{3}$, then the values of $v$ that can be associated with $u=\sqrt[3]{A}$, $u=\omega\sqrt[3]{A}$, $u={\omega}^2\sqrt[3]{A}$ will be $v=\sqrt[3]{B}$, $v=\omega\sqrt[3]{B}$, $v={\omega}^2\sqrt[3]{A}$. Hence, equation (2) will have the following roots: $y_1=\sqrt[3]{A}+\sqrt[3]{B}$, $y_2=\omega\sqrt[3]{A}+{\omega}^2\sqrt[3]{B}$, and $y_3=\omega\sqrt[3]{B}+{\omega}^2\sqrt[3]{A}$. After you find what is the value $A$ and $B$, you back-substitute the $y$s into $x=y-\frac{b'}{3}$ in order to fine the value of $x$.
I will post the discussion about the solutions (Discriminant and how to calculate a special case of the sum of two cube roots that leads to an integer answer as well as irreducible case and how to find the roots in that case.) from the book listed below.
Theory of Equation by Uspensky