I just googled the ##\TeX## for ##\mathcal{D}(\Omega)##, i.e., \mathcal{D}(\Omega).
Apparently ##\mathcal{D}(\Omega)## means a distribution space over an open subset of ##{\displaystyle \mathbb {R}^{n}}##.
The following is excerpted from
https://en.wikipedia.org/wiki/Distribution_(mathematics)
Basic idea
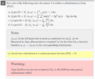
View attachment 239168
A typical test function, the
bump function Ψ(
x).
It is
smooth (infinitely differentiable) and has
compact support (is zero outside an interval,
in this case the interval [−1, 1]).
Distributions are a class of
linear functionals that map a set of
test functions (conventional and
well-behaved functions) into the set of real numbers. In the simplest case, the set of test functions considered is D(
R), which is the set of functions
φ :
R →
R having two properties:
- φ is smooth (infinitely differentiable);
- φ has compact support (is identically zero outside some bounded interval).
A distribution
T is a linear mapping
T : D(
R) →
R. Instead of writing
T(
φ), it is conventional to write ## {\displaystyle \langle T,\varphi \rangle }## for the value of
T acting on a test function
φ. A simple example of a distribution is the
Dirac delta δ, defined by
$${\displaystyle \left\langle \delta ,\varphi \right\rangle =\varphi (0),}$$
meaning that
δ evaluates a test function at 0. Its physical interpretation is as the density of a point source.
As described next, there are straightforward mappings from both
locally integrable functions and
Radon measures to corresponding distributions, but not all distributions can be formed in this manner.
Functions and measures as distributions
Suppose that
f :
R →
R is a locally integrable function. Then a corresponding distribution
Tf may be defined by
$${\displaystyle \left\langle T_{f},\varphi \right\rangle =\int _{\mathbf {R} }f(x)\varphi (x)\,dx\qquad {\text{for}}\quad \varphi \in D(\mathbf {R} ).}$$
This integral is a
real number which depends
linearly and
continuously on ##{\displaystyle \varphi }##. Conversely, the values of the distribution
Tf on test functions in D(
R) determine the pointwise almost everywhere values of the function
f on
R. In a conventional
abuse of notation,
f is often used to represent both the original function
f and the corresponding distribution
Tf. This example suggests the definition of a distribution as a linear and, in an appropriate sense, continuous
functional on the space of test functions D(
R).
Similarly, if μ is a
Radon measure on
R, then a corresponding distribution
Rμ may be defined by
$${\displaystyle \left\langle R_{\mu },\varphi \right\rangle =\int _{\mathbf {R} }\varphi \,d\mu \qquad {\text{for}}\quad \varphi \in D(\mathbf {R} ).}$$
This integral also depends linearly and continuously on ##{\displaystyle \varphi }##, so that
Rμ is a distribution. If μ is
absolutely continuous with respect to Lebesgue measure with density
f and
dμ =
f dx, then this definition for
Rμ is the same as the previous one for
Tf, but if μ is not absolutely continuous, then
Rμ is a distribution that is not associated with a function. For example, if
P is the point-mass measure on
R that assigns measure one to the singleton set {0} and measure zero to sets that do not contain zero, then
$${\displaystyle \int _{\mathbf {R} }\varphi \,dP=\varphi (0),}$$
so that
RP =
δ is the Dirac delta.