- 2,180
- 2,690
##\require{physics}##I am trying to understand how the Ewald's sphere works in the context of X-ray diffraction (XRD). I am reading from Kittel's book, as well as a few lecture series. Let me first state what I have learnt in this context (please correct me if I am wrong).
\mathrm{e}^{i \va{G} \vdot \va{R}} &= 1 \\
\implies \va{G} \vdot \va{R} &= 2\pi m;\ \ m \in \mathbb{Z}.
\end{align}$$ where ##\va{a}_i## are the basis vectors in the real space.
\abs{\va{G}_{hk\ell}} = \dfrac{2\pi}{d_{hk\ell}}
\end{equation}$$ where ##d_{hk\ell}## is the perpendicular distance between to planes with the same Miller indices ##(h, k, \ell).##
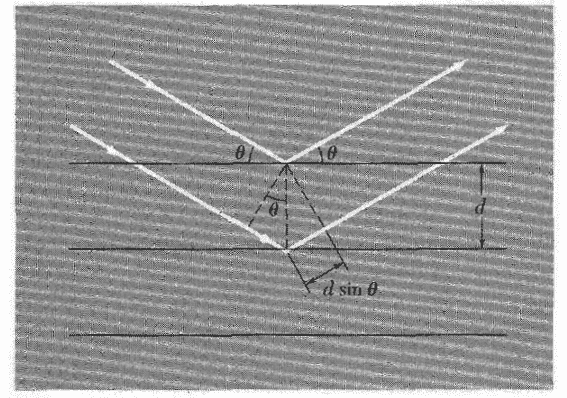
Diffraction of X-rays from the lattice planes.
Source: C. Kittel, Introduction to Solid State Physics, 8th ed. (2014)
2 d_{hk\ell} \sin \theta &= n \lambda;\\
\Delta \va{k} &= \va{G}.
\end{align}$$
With this, let's come to the Ewald's sphere. I will go ahead and copy another diagram from Kittel:

The caption reads:
So, the reciprocal lattice points are basically ##(h, k, \ell).##
These are my questions:
- For any real lattice with translation vector ##\va{R} = n_1 \va{a}_1 + n_2 \va{a}_2 + n_3 \va{a}_3##, we can have a vector in the reciprocal space, defined as
\mathrm{e}^{i \va{G} \vdot \va{R}} &= 1 \\
\implies \va{G} \vdot \va{R} &= 2\pi m;\ \ m \in \mathbb{Z}.
\end{align}$$ where ##\va{a}_i## are the basis vectors in the real space.
- ##\va{G}_{hk\ell} = h \va{g}_1 + k \va{g}_2 + \ell \va{g}_3## is a vector perpendicular to the set of planes in the real space whose Miller indices are given by ##(h, k, \ell);## ##\va{g}_i## are the basis vectors in the reciprocal space.
\abs{\va{G}_{hk\ell}} = \dfrac{2\pi}{d_{hk\ell}}
\end{equation}$$ where ##d_{hk\ell}## is the perpendicular distance between to planes with the same Miller indices ##(h, k, \ell).##
- If ##\va{k}## is the wave vector of the incident X-ray beam, and ##\va{k'}## is the wave vector of the diffracted X-ray, then the scattering vector is ##\Delta \va{k} = \va{k'} - \va{k}.##
Diffraction of X-rays from the lattice planes.
Source: C. Kittel, Introduction to Solid State Physics, 8th ed. (2014)
- The following are equivalent ways of writing Bragg's Law:
2 d_{hk\ell} \sin \theta &= n \lambda;\\
\Delta \va{k} &= \va{G}.
\end{align}$$
With this, let's come to the Ewald's sphere. I will go ahead and copy another diagram from Kittel:
The caption reads:
The points on the RHS are reciprocal lattice points of the crystal. The vector ##\va{k}## is drawn in the direction of the incident X-ray beam, and the origin is chosen such that ##\va{k}## terminates on any reciprocal lattice point (say, A). We draw a sphere of radius $$\abs{\va{k}} = \dfrac{2\pi}{\lambda}$$ about the origin of ##\va{k}##. A diffracted beam will be formed if the sphere intersects any other point in the reciprocal lattice. The sphere, as drawn, intercepts a point (say, B) connected with the end of ##\va{k}## by a reciprocal lattice vector ##\va{G}##. The diffracted beam is in the direction $$\va{k'} = \va{k} + \va{G}.$$ The angle ##\theta## is the Bragg angle of diffraction.
So, the reciprocal lattice points are basically ##(h, k, \ell).##
These are my questions:
- The incident wave vector ##\va{k}## terminates on the point ##A(h_1, k_1, \ell_1).## In the real space, is this the set of lattice planes from where the reflection is taking place?
- If the above is correct, what is the significance of the point ##B(h_2, k_2, \ell_2)## in the real space? This is a different set of planes. What role do these planes play in the diffraction? I understand from geometry that this construction is basically satisfying Bragg's Law in one of the forms stated above. But I couldn't understand the role of the set of planes ##(h_2, k_2, \ell_2)## in the real space.
- Is it possible that the sphere passes through more than two points? If yes, how can we interpret this situation? For instance, if the sphere passes through a third point ##C(h_3, k_3, \ell_3),## we can connect ##A## and ##C## with a different ##\va{G}## vector. And so, there will be reflections in different directions...?