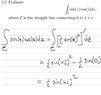Discussion Overview
The discussion revolves around the mathematical expression $\frac{1}{2}(\sin(z))^2$ and its derivation in the context of a line integral, as referenced in an attached image. Participants are attempting to clarify the steps leading to this expression and its relevance to the given path in the solution.
Discussion Character
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant expresses confusion about how the expression $\frac{1}{2}(\sin(z))^2$ is derived and questions the role of the path $C$ in the solution.
- Another participant asserts that the expression $\sin(z)\cos(z)$ relates to $\frac{1}{2}\sin(2z)$ rather than $\frac{1}{2}\sin^2(z)$, indicating a misunderstanding in the initial query.
- A further clarification is requested regarding the transition between steps in the solution process.
- One participant strongly disagrees with the interpretation of the solution, emphasizing that it fails to account for the line integral aspect and that no integration has been performed.
- A later reply mentions that the function $\frac{1}{2}\sin(2z)$ is analytic over the entire complex plane, suggesting that the line integral is path-independent, but does not resolve the initial confusion about the expression.
Areas of Agreement / Disagreement
Participants exhibit disagreement regarding the correct interpretation of the mathematical expressions and the relevance of the line integral. There is no consensus on the steps leading to the expression or the proper treatment of the integral.
Contextual Notes
Participants have not fully resolved the assumptions regarding the derivation of the expression or the implications of the line integral in this context. The discussion reflects varying levels of understanding and interpretation of the mathematical concepts involved.