Understanding Hessian for multidimensional function

  • #1
SaschaSIGI
3
0
Hello everybody,

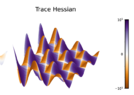
I have a question regarding this visualization of a multidimensional function. Given f(u, v) = e^{−cu} sin(u) sin(v). Im confused why the maximas/minimas have half positive Trace and half negative Trace. I thought because its maxima it only has to be negative. 3D vis

2D visualization
 

Attachments

  • hesse2.PNG
    hesse2.PNG
    37.7 KB · Views: 55
  • hesse1.PNG
    hesse1.PNG
    39.1 KB · Views: 60
Physics news on Phys.org
  • #2
Hi,

You have me wondering what I am looking at. Is the Hessian projected as a color code on a plot of the function ?
Did it occur to you to write down the Hessian for this function ? So: what's the expression for the trace of the Hessian ? (*)

What do you mean with
SaschaSIGI said:
because its maxima it only has to be negative

Aren't there minima between the maxima ?

(by the way: single: minimum, maximum. Plural: minima, maxima)

(*) Notice the similarity with the Laplacian :smile: ?

##\ ##
 

1. What is the Hessian matrix?

The Hessian matrix is a square matrix that contains the second-order partial derivatives of a multivariable function. It is used to determine the curvature and extrema of a function.

2. How is the Hessian matrix calculated?

The Hessian matrix is calculated by taking the second-order partial derivatives of a function and arranging them in a matrix form. The diagonal elements of the matrix represent the second-order partial derivatives with respect to each variable, while the off-diagonal elements represent the mixed partial derivatives.

3. What is the significance of the Hessian matrix in optimization?

The Hessian matrix is used in optimization to determine the nature of the critical points of a function. The positive definiteness of the Hessian matrix at a critical point indicates a local minimum, while a negative definiteness indicates a local maximum. A Hessian matrix with both positive and negative eigenvalues indicates a saddle point.

4. How does the Hessian matrix help in understanding multidimensional functions?

The Hessian matrix provides valuable information about the curvature and extrema of a multidimensional function. By analyzing the eigenvalues and eigenvectors of the Hessian matrix, we can determine the nature of critical points and understand the behavior of the function in different directions.

5. Can the Hessian matrix be used for non-differentiable functions?

No, the Hessian matrix can only be used for differentiable functions. It requires the existence of second-order partial derivatives, which do not exist for non-differentiable functions.

Similar threads

Stationary points classification using definiteness of the Lagrangian
    • Calculus and Beyond Homework Help
Replies
4
Views
842
Function in 3 variables, determinant of the Hessian=0
    • Calculus and Beyond Homework Help
Replies
1
Views
2K
Show Hessian is positive definite
    • Calculus and Beyond Homework Help
Replies
8
Views
6K
Is the Laplacian of a Function Simply the Trace of its Hessian Matrix?
    • Differential Equations
Replies
5
Views
5K
Optimization & singular Hessian matrix
    • Calculus
Replies
2
Views
3K
Mathematica Defining a piecewise function in Mathematica
    • MATLAB, Maple, Mathematica, LaTeX
Replies
2
Views
4K
Challenge Math Challenge - April 2021
    • Math Proof Training and Practice
3
Replies
102
Views
7K
A Understanding the Use of Trace in QFT Lagrangian for Chiral Symmetry in QCD
    • High Energy, Nuclear, Particle Physics
Replies
1
Views
2K
Fortran How Do You Implement MKL's FFT Functions for Multidimensional Data in Fortran?
    • Programming and Computer Science
Replies
2
Views
2K
A Entanglement and density matrix in QFTs
    • High Energy, Nuclear, Particle Physics
Replies
11
Views
2K

Hot Threads

Recent Insights

Back
Top