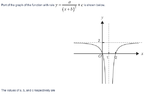
Let's make this really interesting by choosing some suitably large values for $x$.
Let's see what happens at $x = 1,000,000$, when $a = b = -1,c = 2$.
Then $f(x) = \dfrac{-1}{(999,999)^2} + 2$
$= \dfrac{-1}{999,998,000,001} + 2$
$\sim 1.999999999998999998$
At $x = -1,000,000$, we get:
$f(x) = \dfrac{-1}{(-1,000,001)^2} + 2$
$= \dfrac{-1}{1,000,002,000,001} + 2$
$\sim 1.999999999999000002$
Both of these numbers are really close to 2, right?
In general, we see that:
$\displaystyle \lim_{x \to \infty} \left(\frac{a}{(x + b)^2} + c\right)$
$\displaystyle = \lim_{x \to \infty} \frac{a}{(x + b)^2} + \lim_{x \to \infty} c$
$\displaystyle = \lim_{x \to \infty} \frac{a}{(x+b)^2} + c$
$\displaystyle = (a)\left(\lim_{x \to \infty}\frac{1}{x+b}\right)^2 + c$
$\displaystyle = (a)(0)^2 + c = 0 + c = c$
Similar reasoning holds to show that:
$\displaystyle \lim_{x \to -\infty} \left(\frac{a}{(x + b)^2} + c\right) = c$
as well.
(If you haven't been formally introduced to limits yet, all you need to know for this is the following (which hold under "suitably nice conditions" which are the case here):
1) the limit of a sum is the sum of the limits of each term in the sum
2) the limit of a product is the product of the limits of each factor in the product
3) if M(x) is a function that gets "infinitely big" as x does, then:
$$\lim_{x \to \infty} \frac{1}{M(x)} = 0$$
-by "get infinitely big as x does" I mean that for ANY positive integer $K$, there is always some positive integer $N$, so that if we have $x > N$, then $|M(x)| > K$ (typically, the integer $N$ will depend on $K$, bigger $K$'s usually need bigger $N$'s).).