Understanding Momentum Eigenfunctions in Quantum Mechanics

[hmm.max]

I'm not sure if this is what you're looking for, but here's a simple answer-

Even in situations with NO potential energy anywhere, energy eigenstates are not generally momentum eigenstates. A particle's kinetic energy depends on the magnitude, but not the direction of its momentum. So most energy eigenstates are linear combinations of many different momentum eigenstates with the same magnitude but different direction.

In a one-dimensional situation, there are only two directions, positive and negative. So a standing wave like

psi = A sin( k x ) = A/2i ( e^(i k x) - e^(-i k x)

is a superposition of TWO momentum eigenstates, one in each direction. The energy states for the infinite square well have this form. They aren't eigenstates of momentum.

 

[hmm.max]

What I meant was, since inside the well the potential energy is zero, there is a one-to-one relation between the discrete momentum states and the discrete energy states.

You may have resolved this already, but to elaborate on what I just said, there isn't a one to one correspondence, even for zero potential energy. There are many different momentum states with the same energy. So in general, energy states are superpositions of different momentum states. For square potential wells, the wave functions must be standing waves, which means they must always be linear superpositions of at least two momentum states with opposite directions.

Hope this is relevant to something.

-max

 

[snoopies622]

In a one-dimensional situation, there are only two directions, positive and negative. So a standing wave like

psi = A sin( k x ) = A/2i ( e^(i k x) - e^(-i k x)

is a superposition of TWO momentum eigenstates, one in each direction.

Yes, this makes complete sense to me. But two momentum eigenstates is not a continuum of them.

 

[snoopies622]

Energy eigenfunctions are sinusoidal waves in the well and are zero outside.

So you're saying that a simple sine wave like

\psi (x) = sin (kx) = sin ( \frac { \sqrt {2mE} } {\hbar} x )

that goes on forever in both directions - that is, is not bounded at two x values like the ones in the examples - is not an energy eigenfunction?

Edit: Perhaps I should have made

\psi (x) = e ^ {ikx} = e ^{ i( \frac { \sqrt {2mE} } {\hbar} x )}

 

[sweet springs]

Hi, hmm.max

There are many different momentum states with the same energy.

In general case that there exists potential energy, momentum and energy do not commute. Momentum state cannot have definite energy value. Thus it is not appropriate to refer same energy or not.

For square potential wells, the wave functions must be standing waves, which means they must always be linear superpositions of at least two momentum states with opposite directions.

Instead let me say, for energy eigenstates in square potential well of infinite depth, the wave functions must be standing waves WITHIN THE WELL AND ZERO OUTSIDE, which means they must always be linear superpositions OF CONTINUOUS INTEGRALS OF momentum states THAT EACH ONE IS NOT BOUNDED AT TWO VALUES.　Think of Fourier transform please.

Hi, snoopies622.

So you're saying that a simple sine wave like
\psi (x) = sin (kx) = sin ( \frac { \sqrt {2mE} } {\hbar} x )

that goes on forever in both directions - that is, is not bounded at two x values like the ones in the examples - is not an energy eigenfunction?

No, it is not an energy eigenfunction of infinite depth square well potential. Why such an idea is haunting on you? Imagine particle can be outside the well as you say. There potential energy is infinite thus the eigenvalue of this eigenstate cannot be finite. Is this acceptable?

PS
In order to avoid misunderstanding it would be helpful to write wave function of energy eigenstate in the infinite square well potential system as ψ (x) = sin (kx) Θ(x) = 1/2i e^ikx Θ(x) - 1/2i e^-ikx Θ(x) where support Θ(x)=1 within the well region, 0 for outside.
sin (kx) Θ(x), not sin (kx), is energy eigenfunction.
e^ikx, not e^ikxΘ(x), is momentum eigenfunction.

Regards.

 

[hmm.max]

of course, i completely agree, sweet springs. in a non-zero potential, momentum eigenstates don't have definite energy. i was first talking specifically about the case of zero potential, in order to address the difference between a sinusoidal wave function and a momentum eigenstate, in concrete terms.

and yes, for a square potential well, many (infinite) more than two momentum components are required to represent the actual wave function, because it goes to zero outside the well. this is true. i should have focused that comment on standing waves in general, rather than on the energy states of the square well.

 

[hmm.max]

So you're saying that a simple sine wave like

\psi (x) = sin (kx) = sin ( \frac { \sqrt {2mE} } {\hbar} x )

that goes on forever in both directions - that is, is not bounded at two x values like the ones in the examples - is not an energy eigenfunction?

Edit: Perhaps I should have made

\psi (x) = e ^ {ikx} = e ^{ i( \frac { \sqrt {2mE} } {\hbar} x )}

Yeah those are eigenfunctions of the "free particle" hamiltonian (where V = 0 everywhere), but not of the infinite square well hamiltonian.

 

[snoopies622]

Since V(x)=0 inside the well, all this time I've been using

<br /> <br /> - \frac { \hbar ^2} {2m} \frac {\partial ^2 }{ \partial x ^2 }<br /> <br />

as the energy operator instead of

<br /> <br /> - \frac { \hbar ^2} {2m} \frac {\partial ^2 }{ \partial x ^2 } + V (x)<br /> <br /> \vspace {5 mm}.

 

[hmm.max]

In order to avoid misunderstanding it would be helpful to write wave function of energy eigenstate in the infinite square well potential system as ψ (x) = sin (kx) Θ(x) = 1/2i e^ikx Θ(x) - 1/2i e^-ikx Θ(x) where support Θ(x)=1 within the well region, 0 for outside.
sin (kx) Θ(x), not sin (kx), is energy eigenfunction.
e^ikx, not e^ikxΘ(x), is momentum eigenfunction.

Regards.

That's a good way of putting it.

 

[sweet springs]

Hi, snoopies622

Since V(x)=0 inside the well,

How about wave function outside the well? Does it keep to be a sinusoidal wave?
Regards.

 

[snoopies622]

No, ψ (x) = 0 outside the well.

 

[snoopies622]

No, it is not an energy eigenfunction of infinite depth square well potential. Why such an idea is haunting on you?

I understand now, sweet springs. Ψ(x) can be defined in a piecewise manner to solve the Schrodinger equation using the piecewise-defined potential, and this yields energy values, not momentum values. Thank you for all of your efforts.

Here's a follow-up question for you, and it's been at the root of all my confusion in this particle-in-a-box matter. Since inside the box there isn't a one-to-one (or two-to-one) relation between momentum states and energy states, isn't it odd that the method I described in entry #18 for finding the discrete energy values works? It assumes discrete momentum values, then squares them and divides by 2m.

 

[Dickfore]

The nth stationary state is:

<br /> \psi_{n}(x) = \left\{\begin{array}{cl}<br /> \sqrt{\frac{2}{L}} \, \sin\left(\frac{n \pi x}{L}\right) &amp;, \ 0 \le x \le L \\<br /> <br /> 0 &amp;, x &lt; 0 \vee x &gt; L<br /> \end{array}\right., \ n = 1, 2, \ldots<br />

The momentum eigenfuniction is:

<br /> \phi_{p}(x) = \frac{1}{(2 \pi \hbar)^{1/2}} \, e^{\frac{i \, p \, x }{\hbar}}, \ -\infty &lt; x &lt; \infty<br />

These momentum eigenfunctions (plane waves) form a complete orthonormal basis of functions and we can expand any function in them. Let us expand the nth stationary state from above. The expansion is actually an integral and the coefficient is a function of the continuous parameter p:

<br /> a(p) = \int_{-\infty}^{\infty}{\phi^{\ast}_{p}(x) \, \psi_{n}(x) \, dx}<br />

<br /> a(p) = \frac{1}{(2 \pi \, \hbar)^{1/2}} \, \left(\frac{2}{L}\right)^{1/2} \, \frac{1}{2 i} \left[ \int_{0}^{L}{\exp(i (\frac{n \pi}{L} - \frac{p}{\hbar}) \, x) \, dx} - \int_{0}^{L}{\exp(-i (\frac{n \pi}{L} + \frac{p}{\hbar}) \, x) \, dx}\right]<br />

<br /> a(p) = \frac{1}{2 i} \left( \frac{1}{\pi \hbar L} \right)^{1/2} \left[\frac{1}{i (\frac{n \pi}{L} - \frac{p}{\hbar})} - \frac{1}{-i (\frac{n \pi}{L} + \frac{p}{\hbar})}\right] \, ((-1)^{n} exp(-i \frac{p \, L}{\hbar}) - 1)<br />

<br /> a(p) = \frac{n \, \pi}{L} \left(\frac{1}{\pi \, \hbar \, L} \right)^{1/2} \, \frac{1 - (-1)^{n} \exp(-i \, \frac{p \, L}{\hbar})}{(\frac{n \, \pi}{L})^{2} - (\frac{p}{\hbar})^{2}}<br />

The square of the absolute value of these complex numbers gives the probability density for dfifferent values of p. The only complex number is the expression in the numerator. We evaluate its square absolute value as:
<br /> \begin{array}{l}<br /> \left| 1 - (-1)^{n} \exp(-i \, \frac{p \, L}{\hbar}) \right|^{2} = \left( 1 - (-1)^{n} \exp(-i \, \frac{p \, L}{\hbar})\right) \left( 1 - (-1)^{n} \exp(i \, \frac{p \, L}{\hbar})\right) \\<br /> <br /> =1 - (-1)^{n} \exp(-i \, \frac{p \, L}{\hbar}) - (-1)^{n} \exp(i \, \frac{p \, L}{\hbar}) + 1 \\<br /> <br /> = 2 \left[ 1- (-1)^{n} \, \cos\left(\frac{p \, L}{\hbar}\right)\right]<br /> \end{array}<br />

<br /> |a(p)|^{2} = \frac{\frac{n^{2} \, \pi}{\hbar \, L{3}}}{\left(\frac{\pi}{L}\right)^{4}} \, \frac{2 \left[ 1- (-1)^{n} \, \cos\left(\frac{p \, L}{\hbar}\right)\right]}{\left[n^{2} - \left(\frac{p \, L}{\hbar \pi}\right)^{2}\right]^{2}}<br />

<br /> |a(p)|^{2} = \frac{L}{\hbar \, \pi} \, \frac{2 \left(\frac{n}{\pi}\right)^{2} \, \left[1 - (-1)^{n} \, \cos\left( \pi \, \frac{p \, L}{\hbar \, \pi}\right) \right]}{\left[n^{2} - \left(\frac{p \, L}{\hbar \pi}\right)^{2}\right]^{2}}<br />

The denominator has double zeros for:

<br /> \tilde{p} \equiv \frac{p \, L}{\hbar \, \pi} = \pm n<br />

These values correspond to the values for momentum that give "standing De Broglie's waves" with nodes at the walls of the potential well. However, the numerator is also zero for these values and the limit 0/0 can be evaluated by using the L'Hospital's Rule:

<br /> |a(\tilde{p}_{n})|^{2} = \frac{1}{4} \, \frac{L}{\hbar \, \pi}<br />

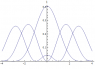
The plot of this probability distribution is given on the graph below (for n = 1, 2, 3):

As you can see, the distribution has a non-zero, but finite probability density any other (continuous) value for \tilde{p} as well.

 

[snoopies622]

Hey thanks, Dickfore! I had no idea how to calculate those coefficients.

 

[sweet springs]

Hi, snoopies622.

It assumes discrete momentum values, then squares them and divides by 2m.

To adjust discrete wavelength according to the size of well or box should not be regarded as momentum fitting. de Broglie relation h'/λ=p applies to waves of infinite length, not to waves of finite length or wave train. In order to know what momentum wave train has, we have to decompose it to momentum eigenstates by Fourier transform. However even wave train, square of h'/λ gives energy multiplied by 2m in the well where V=0.
Regards.

 

[snoopies622]

The momentum eigenfunction is:

<br /> \phi_{p}(x) = \frac{1}{(2 \pi \hbar)^{1/2}} \, e^{\frac{i \, p \, x }{\hbar}}, \ -\infty &lt; x &lt; \infty<br />

These momentum eigenfunctions (plane waves) form a complete orthonormal basis of functions and we can expand any function in them.

I have a couple questions about this:

1. Why are these vectors not dimensionless? (or are you using a system of units such that Planck's constant is just a number?)

2. What does it mean to say that they are orthonormal? I understand what "orthonormal" means when it refers to a finite-dimensional vector space like \bold {R}^3, and I understand how these vectors are "ortho" at least in the sense that are linearly independent. But what about the "normal" part? Is there a sense in which a sine wave can have unit length?

Thanks.

 

[Dickfore]

1. Why are these vectors not dimensionless? (or are you using a system of units such that Planck's constant is just a number?)

2. What does it mean to say that they are orthonormal? I understand what "orthonormal" means when it refers to a finite-dimensional vector space like \bold {R}^3, and I understand how these vectors are "ortho" at least in the sense that are linearly independent. But what about the "normal" part? Is there a sense in which a sine wave can have unit length?

Eigenfunctions are never dimensionless. In accordance with the probabilistic interpretation of
the wave function, when a particle is in a state described by the wave function \Phi(\mathbf{r}), then |\Phi(\mathbf{r})|^{2} \, d^{d}r is the probability of finding the particle in the infinitesimal volume dV = d^{d}r (d is the dimensionality of space) around the point with position vector \mathbf{r}. SInce probabilities are dimensionless quantities, from here it immediately follows that the dimension of the wavefunction is:

<br /> [\Phi]^{2} \, \mathrm{L}^{d} = 1 \Rightarrow [\Phi] = \mathrm{L}^{-\frac{d}{2}}<br />

Since the total probability of finding the particle somewhere in space must be one, the wave functions ought to be normalized:

<br /> \int{|\Phi(\mathbf{r})|^{2} \, d^{d}r} = 1<br />

Orthonormal is a shorthand amalgamation of two terms coined by lazy physicists :) It stands for orthogonal and normalized.

For observables with continuous spectra (such as momentum), one has to be careful what is meant by "normalization", since the eigenfunctions are not square-integrable. When we say the momemtnum eigenfunctions are orthonormal, we mean they satisfy the following identity:

<br /> \int{\psi^{\ast}_{\mathbf{p}}(\mathbf{r}) \, \psi_{\mathbf{p}&#039;}(\mathbf{r}) \, d^{d}r} = \delta^{(d)}(\mathbf{p} - \mathbf{p}&#039;)<br />

where

<br /> \delta^{(d)}(\mathbf{p} - \mathbf{p}&#039;) = \prod_{i = 1}^{d} {\delta(p_{i} - p&#039;_{i})}<br />

is the d-dimensional Dirac delta-function, with \delta(p_{i} - p&#039;_{i}) being the continuum generalization of the Kronecker delta \delta_{m, n}. A Dirac delta-function has the following fundamental property:

<br /> \int_{-\infty}^{\infty}{f(x&#039;) \, \delta(x -x&#039;) \, dx&#039;} = f(x)<br />

as a direct generalization of the discrete case:

<br /> \sum_{m = -\infty}^{\infty}{f_{m} \, \delta_{n, m}} = f_{n}<br />

(the index n goes to the continuous label x, a sequence f_{n} goes to a function f(x) and summation over m goes to integration over x&#039;:

<br /> \begin{array}{rcl}<br /> n &amp; \rightarrow &amp; x \\<br /> <br /> f_{n} &amp; \rightarrow &amp; f(x) \\<br /> <br /> \sum_{m = -\infty}^{\infty}{(\ldots)_{m}} &amp; \rightarrow &amp; \int_{-\infty}^{\infty}{dx&#039; \, (\ldots)(x&#039;)}<br /> \end{array}<br />

From the fundamental property of the delta function, one can specficially see that its dimension is the reciprocal of that of its variable x:

<br /> [\delta(x)] = [x]^{-1}<br />

Specifically, for [\delta^{(d)}(\mathbf{p} - \mathbf{p}&#039;)] = [\delta(p)]^{d} = [p]^{-d}, and, from the orthonormality condition of the momentum eigenfunctions from above, we get:

<br /> [\psi_{\mathbf{p}}(\mathbf{r})]^{2} \, \mathrm{L}^{d} = [p]^{-d} \Rightarrow<br /> <br /> [\psi_{\mathbf{p}}(\mathbf{r})] = ([p] \, \mathrm{L})^{-\frac{d}{2}}<br />

Using the fact that:

<br /> [p] \, \mathrm{L} = \mathrm{M} \, \mathrm{L}^{2} \, \mathrm{T}^{-1} = [\hbar]<br />

we see that:

<br /> [\psi_{\mathbf{p}}(\mathbf{r})] = [\hbar]^{-\frac{d}{2}}<br />

and the above formula for the momentum eigenfunctions is dimensionally correct (d = 1 there). The factor of 2 \pi comes from the formulas:

<br /> \int_{-\infty}^{\infty}{e^{i \, k \, x} dx} = 2\pi \, \delta(k)<br />

<br /> \delta(a \, k) = \frac{1}{|a|} \, \delta(k)<br />

 

[snoopies622]

Thanks again, Dickfore. I'm going to have to look into Fourier transforms a little more.

 

[snoopies622]

When we say the momentum eigenfunctions are orthonormal, we mean they satisfy the following identity:

<br /> \int{\psi^{\ast}_{\mathbf{p}}(\mathbf{r}) \, \psi_{\mathbf{p}&#039;}(\mathbf{r}) \, d^{d}r} = \delta^{(d)}(\mathbf{p} - \mathbf{p}&#039;)<br />

I take it then that

<br /> <br /> \int ^ {\infty} _ {-\infty} sin (x) dx = 0 \hspace {5 mm} ?<br /> <br />

(And likewise for cosine.)

 

[Dickfore]

I take it then that

<br /> <br /> \int ^ {\infty} _ {-\infty} sin (x) dx = 0 \hspace {5 mm} ?<br /> <br />

(And likewise for cosine.)

Strictly speaking, these intergrals are not defined in the sense of Riemann integrable. However, if you consider the Gaussian integral:

<br /> \int_{-\infty}^{\infty}{\exp\left[i \beta x - \frac{a x^{2}}{2}\right] \, dx} = \sqrt{\frac{2 \pi}{a}} \, \exp\left(-\frac{\beta^{2}}{2 a}\right), \ a &gt; 0<br />

and is well behaved for the stated values of a.

Furthermore, taking a \rightarrow 0^{+} recovers an integrand on the left hand side whose real and imaginary parts give the integrals you are interested in. However, the right hand side does not have a limit. You need the definition of Dirac delta-function through limits to express it:

<br /> \delta(x) = \lim_{\lambda \rightarrow 0}{\frac{1}{\sqrt{2 \pi} \lambda} \, e^{-\frac{x^{2}}{2 \lambda^{2}}}}<br />

Taking \lambda = \sqrt{a}, we see that the right hand side of the above integral tends to:

<br /> 2\pi \, \delta(\beta), \ a \rightarrow 0^{+}<br />

So, we can write:

<br /> \int_{-\infty}^{\infty}{e^{i \beta x} \, dx} = 2\pi \, \delta(\beta)<br />

Taking the real and imaginary part of this equality, we have:

<br /> \begin{array}{l}<br /> \int_{-\infty}^{\infty}{\sin(\beta x) \, dx} = 0 \\<br /> <br /> \int_{-\infty}^{\infty}{\cos(\beta x) \, dx} = 2\pi \, \delta(\beta)<br /> \end{array}<br />

Taking \beta = 1, you get that even the cosine integral is zero (the sine is an integral of an odd function on a symmetric interval, so it should always be zero).

 

[snoopies622]

Wow, thanks Dickfore. Good stuff.