Homework Help Overview
The discussion revolves around RLC circuits, specifically comparing series and parallel configurations. Participants are exploring the relationships between current and voltage in these circuits, particularly focusing on the behavior of inductors and capacitors.
Discussion Character
- Exploratory, Conceptual clarification, Assumption checking
Approaches and Questions Raised
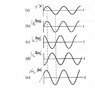
- Participants are questioning the correctness of current equations for series and parallel RLC circuits. There is a focus on understanding the negative sign in the inductor current equation and the differences in current relationships for inductors and capacitors. Some participants suggest sketching current and voltage relationships to clarify these concepts.
Discussion Status
The discussion is active, with participants providing insights and raising questions about the relationships between circuit components. Some guidance has been offered regarding the mathematical relationships and the importance of defining variables clearly. There is an acknowledgment of the need for clarity in circuit diagrams and variable definitions.
Contextual Notes
Participants note the importance of polarity in current direction and the definition of variables used in their equations. There is mention of a specific current, ΔIL, which has not been clearly defined, leading to further questions about its relevance in the context of parallel RLC circuits.