Understanding Tension Forces: How to Calculate and Measure Them

[BadSkittles]

Hello everyone, I am puzzled by how the sum of the tension forces on a rope is calculated.

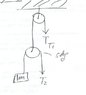
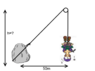
So let's say a climber (5kg) is dangling on a cliff, with a rope around his waist. That same rope is wrapped around a rock (10 kg) 50 meters left of the cliff. How would the tension force of that rope be measured when the rope goes in different directions.

What about a pulley? Is the tension force just the sum of the mass * gravity?

Also, what is the equation for tension forces. Is it just the sum of all forces that the rope is tugged by?

Help is much appreciated

 

[rock.freak667]

There is no fixed formula for tension. You would normally get the tension based on equilibrium conditions.

So if the 5 kg climber (that is quite small btw) is just hanging there then the tension is balancing the weight vertically so T = (5*9.81) N.

If there are two ropes and he is stationary, then the components of the tensions in the x and y directions will need to be balanced.

 

[barryj]

If a rope goes over a FRICTIONLESS pully, then the tension of the rope will be the same on both sides of the pully. It wouldn't matter what direction of the rope took.

 

[voko]

If a rope goes over a FRICTIONLESS pully, then the tension of the rope will be the same on both sides of the pully. It wouldn't matter what direction of the rope took.

Frictionless AND massless.

 

[Chestermiller]

Frictionless AND massless.

If the system is in static equilibrium, then the mass of the pulley is irrelevant.

 

[voko]

If the system is in static equilibrium, then the mass of the pulley is irrelevant.

This is an oversimplification. The weight of a pulley might be relevant even statically.

 

[Chestermiller]

This is an oversimplification. The weight of a pulley might be relevant even statically.

Please give an example of how this can be the case for a frictionless pulley.

Chet

 

[barryj]

See attachment. Here T1 = T2 + mg

 

[Chestermiller]

See attachment. Here T1 = T2 + mg

This does not address the issue that Voko and I were discussing.

 

[barryj]

I thought you were asking for an example of a static situation with a frictionless pulley where mass mattered. Sorry, I guess I misunderstood the question.

 

[barryj]

Chester, what was "the issue that Voko and I were discussing." I should have said that..
T1 = T2 + mg + (mass of pulley)g

 

[voko]

This does not address the issue that Voko and I were discussing.

I am not sure what particular issue you have in mind. My comment was generic, the mass of a pulley may not always be neglected even in static equilibrium. I believe the diagram supplied by barryj illustrates that.

 

[Chestermiller]

I am not sure what particular issue you have in mind. My comment was generic, the mass of a pulley may not always be neglected even in static equilibrium. I believe the diagram supplied by barryj illustrates that.

What I was saying was that, for a frictionless pulley situated within a system under static equilibrium conditions, the cord tension on one side of the pulley is the same as the cord tension on the other side of the pulley, irrespective of whether the pulley has mass. Maybe I should have been more precise in what I said.

Chet

 

[voko]

Yes, that is true. If the tensions were different, the pulley would have a non-zero net torque acting on it.

 

[CWatters]

So let's say a climber (5kg) is dangling on a cliff, with a rope around his waist. That same rope is wrapped around a rock (10 kg) 50 meters left of the cliff. How would the tension force of that rope be measured when the rope goes in different directions

Something like this? If not then please post your own diagram...

The man creates a tension = M_mg in the rope. Where M_m is the mass of the man and g is the acceleration due to gravity. The tension in the rope the other side is the same.

Some of that tension (the horizontal component) is countered by friction between rock and ground.

Some of that tension (the vertical component) is countered by gravity acting on the rock.

What fraction of the total does what depends on the angle and you didn't specify "h" so we can't work out the angle.

 

[haruspex]

the mass of a pulley may not always be neglected even in static equilibrium. I believe the diagram supplied by barryj illustrates that.

This is a little unfair. The original point under discussion was specifically whether the mass of a pulley can lead to a difference in tension in the sections of rope with which it makes contact:

If a rope goes over a FRICTIONLESS pully, then the tension of the rope will be the same on both sides of the pully

In statics, it doesn't, though its weight may contribute to tension in other parts of the system, or increase the tension equally both sides of itself.

 

[voko]

This is a little unfair. The original point under discussion was specifically whether the mass of a pulley can lead to a difference in tension in the sections of rope with which it makes contact:

I am not exactly sure what the "original point" really is. The original post does not specifically restrict the discussion to statics, that may at best only be inferred from it. The initial post of Chestermiller had a statement in such a form ("mass is irrelevant") that I did not realize it was strictly about the equality of tensions.

Anyway, I think I have addressed both the generic and the static cases explicitly.

 

[haruspex]

I am not exactly sure what the "original point" really is..

I was referring to the point made in post #3 and the discussion that engendered starting with your #4.