ali PMPAINT
- 44
- 8
- Homework Statement
- arctan(1)+arctan(2)+arctan(3)=Pi
- Relevant Equations
- I think tan(a)+tab(b)+tan(c)=tan(a)*tan(b)*tan(c)
So, I saw the answer but I couldn't understand it. But I think it can be solved by tan(a)+tab(b)+tan(c)=tan(a)*tan(b)*tan(c) (where a+b+c=Pi) , but I don't know how to transfer it to its inverse.
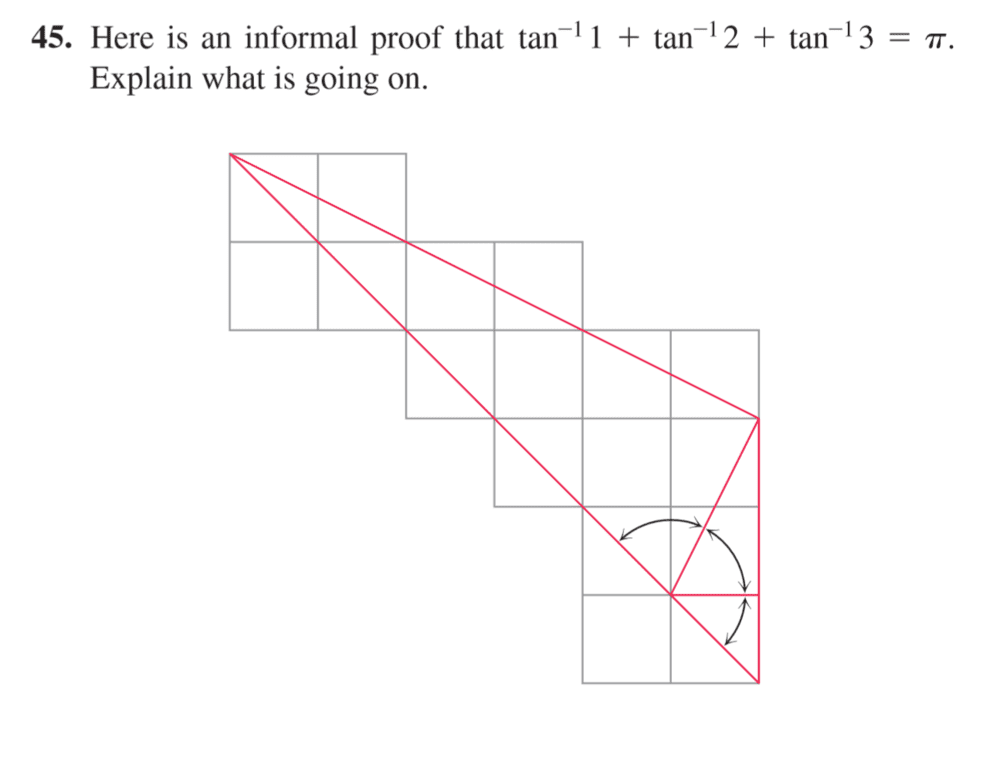
The answer:
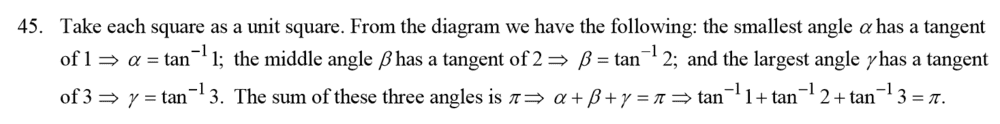
The answer:
 ##\qquad## !
##\qquad## !