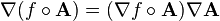SUMMARY
This discussion focuses on the application of the chain rule in vector calculus for calculating the gradient of scalar functions, specifically in the context of a vector A defined as A = [a(x,y,z) hat;x + b(x,y,z) hat;y + c(x,y,z) hat;z]. The expression for the gradient of f(A) is derived using the chain rule, resulting in the formula: ∇ f(A) = hat;x (∂f/∂x)(∂a/∂x + ∂b/∂x + ∂c/∂x) + hat;y (∂f/∂y)(∂a/∂y + ∂b/∂y + ∂c/∂y) + hat;z (∂f/∂z)(∂a/∂z + ∂b/∂z + ∂c/∂z). The discussion also touches on the notation used for partial differentiation and the implications of expressing the gradient in different coordinate systems.
PREREQUISITES
- Understanding of vector calculus concepts, particularly gradients.
- Familiarity with scalar functions and their derivatives.
- Knowledge of partial differentiation notation and operations.
- Basic comprehension of coordinate transformations, including spherical coordinates.
NEXT STEPS
- Study the application of the chain rule in different coordinate systems, focusing on spherical coordinates.
- Explore the concept of gradient fields and their physical interpretations in vector calculus.
- Learn about matrix representations of gradients and their applications in multivariable calculus.
- Investigate advanced topics in vector calculus, such as divergence and curl, and their relationship to gradients.
USEFUL FOR
Students and professionals in mathematics, physics, and engineering who are looking to deepen their understanding of vector calculus, particularly in the context of gradients and scalar functions.