LCSphysicist
- 644
- 163
- Homework Statement
- .
- Relevant Equations
- .
I am extremelly confused with this question: Basically suppose we have two electric dipoles, parallel to each other, as follows in the figure:
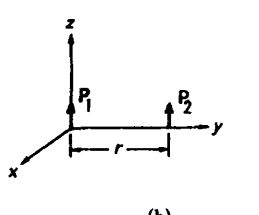
I am supposed to show that the force is attractive and radial. But I am not getting how it can be radial (pointing toward each other)!
See, the force acting on a dipole is $$\vec F = (\vec p \cdot \vec \nabla ) \vec E$$
So the force is parallel to the electric field. Let's consider the force acting on $P1$ due to $P2$
But, here, $$\vec E = k\frac{3(\vec p . \vec r) \vec r - \vec p}{r^5} = \frac{-p_2}{4 \pi \epsilon r^3} \hat z$$
And, since ##\hat z## is constant, ##(\vec p \cdot \vec \nabla)## will not alter its direction, so the force is also in z direction !?
I am almost sure i am misinterpretating the electric field equation and i have not noticed that, since this formula was right in all the ways i have used it
I am supposed to show that the force is attractive and radial. But I am not getting how it can be radial (pointing toward each other)!
See, the force acting on a dipole is $$\vec F = (\vec p \cdot \vec \nabla ) \vec E$$
So the force is parallel to the electric field. Let's consider the force acting on $P1$ due to $P2$
But, here, $$\vec E = k\frac{3(\vec p . \vec r) \vec r - \vec p}{r^5} = \frac{-p_2}{4 \pi \epsilon r^3} \hat z$$
And, since ##\hat z## is constant, ##(\vec p \cdot \vec \nabla)## will not alter its direction, so the force is also in z direction !?
I am almost sure i am misinterpretating the electric field equation and i have not noticed that, since this formula was right in all the ways i have used it