Understanding the size of the angle

[Vital]

Homework Statement

Hello!
Please, take a look at the exercise I post below. I have solved it correctly, and I understand how to solve it; so no problems here. But what I do have a problem with is the size of the angle between two points. Please, see details below. I will be grateful for your help and explanation.

Homework Equations

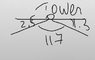
From a point 300 feet above level ground in a firetower, a ranger spots two fires in the Yeti National Forest. The angle of depression made by the line of sight from the ranger to the first fire is 2.5° and the angle of depression made by line of sight from the ranger to the second fire is 1.3°. The angle formed by the two lines of sight is 117°. Find the distance between the two fires.

The Attempt at a Solution

I found the correct distance, no issues here (it's around 17455), but how can the angle between two lines of sight be equal to 117°, if one angle of depression is 2.5° and another is 1.3°, which if combined are only 3.8°.
180° - 3.8° is far from 117°. See my "drawing" attached.

How can that angle be 117°?
Thank you!

 

[Daniel Gallimore]

From your drawing, it looks like you are trying to fit all of the angles into the same plane. Instead, let the angle of depression represent the amount by which the ranger looks down, not side to side. If the ranger looks down $2.5^\circ$ in one direction, turns through some unspecified angle, then looks down $1.3^\circ$ in another direction, his two lines of sight will define a plane. The angle between those lines of sight within that plane is $117^\circ$. You want to find the distance between where those lines of sight encounter the flat ground, a vertical distance $300$ feet below the ranger.

 

[ehild]

T represents the tower, A and B are the fires. OAB triangle is horizontal, OAT and OBT triangles are vertical. You have to find the distance between A and B, from the triangle ABT.

 

[Vital]

View attachment 199364
T represents the tower, A and B are the fires. OAB triangle is horizontal, OAT and OBT triangles are vertical. You have to find the distance between A and B, from the triangle ABT.

What a nice picture. How did you create it?
I am fine with finding the sides, as I have pointed out - I did solve the task, using right angles to find sides.

But thanks to both explanations, I see my mistake. Indeed I did fit both angles into the same plane, which is not right, as I see now.
The only point I would like to make regarding the picture above: the guy is at the point T watching downwards, hence the angle of depression would be the one formed by TA and a horizontal line parallel to the ground at T level (like the one I have on my picture), and that's how this is explained in the book. This would mean that ∠TAB equals 2.5° also as both angles are congruent.

 

[ehild]

What a nice picture. How did you create it?

With Paint.

The only point I would like to make regarding the picture above: the guy is at the point T watching downwards, hence the angle of depression would be the one formed by TA and a horizontal line parallel to the ground at T level (like the one I have on my picture), and that's how this is explained in the book. This would mean that ∠TAB equals 2.5° also as both angles are congruent.

The angle of TA with the horizontal at point T ( in the direction of fire A) is the same as the angle between TA and OA (on the ground) <TAB is not 2.7°.