Understanding Trigonometric Equations with Infinite Solutions

[PhotonW/mass]

Hello I was trying to solve this sample problem, but I really don't get it.
The book says this word by word:

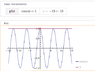
The equation sin3x=1 implies

3x=(pi/2)+2kpi, k an integer.
x= (pi/6)+(2kpi/3), k an integer *Divide each side by 3.

Because x is not restricted to a finite interval, the given equation has an infinite number of solutions. All the solutions are represented by the equation

x= (pi/6)+2kpi/3


Okay it lost me when it told me 3x=(pi/2)+2kpi.
I am really confused. This is not solved like the rest of the trigonometric equations.

 

[sz0]

Hi, since the trigonometric functions are periodic there is more than one answer to what 3x can equal to sole your equation.
sin(v) = 1 implies v = pi/2 , but but pi/2 + 2*pi or pi/2 + 4*pi will do as well since it is 2pi-preiodic. k represents any number, that is k = 0,+-1,+-2,+-3 etc.

So therefor v = 3x = pi/2 + k*2pi which gives x= (pi/6)+(2kpi/3)

if x had been restricted then like for example 0<x<2*pi then only x = pi/6 had been an acceptable answer.

 

[saplingg]

Hi,

As the previous poster said, consider the fact that the trig functions are periodic.
The cosine function can be called a "many-to-one" function.

So let's think about the function f(x) = cos(x).

Let me ask you, for what values of x does cos(x) = 1? If you can imagine the graph of the cosine function, or maybe the unit circle, you could tell me: cos(0) = 1.

But also, cos(-4π) = cos(-2π) = cos(2π) = cos(4π) = 1.

Therefore, we can say that solutions of x for the equation, are 2π * k, for some integer k.​

Look at the picture I attached for a view of this.
https://www.physicsforums.com/attachment.php?attachmentid=57974&stc=1&d=1366232397



Now, let's apply the same idea to your original question:

sin(3x) = 1
What values of (3x) does sin(3x) = 1?
Well, an obvious one is 3x = π/2, but also 3x = 5π/2, 9π/2 ...

We can apply the same notation, 3x = π/2 + 2π * k
​

Hope this helps.