Uniform right circular cone hanging in equilibrium

[Taniaz]

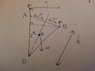
1. A uniform right circular solid cone of weight W is suspended by two vertical strings attached to the ends A and B of a diameter of its base. If the cone hangs in equilibrium with its vertex vertically below A, find the tension in the strings.

2. Centre of mass of cone from the vertex is 3/4 h
Moments formula

3. I understand we have to take moments to find the tension but 1) I'm not sure if the tension in both strings is the same 2) since the vertex is vertically below A, I'm not sure what the horizontal distance from the weight to A and B is to be able to use moments. I know that the c.o.m of the cone lies at 3/4 h from the vertex but not sure what the coordinates will be in this case and I assume you require the x-coordinate for the horizontal distance .

 

[BvU]

1) definitely not
2) make a drawing
You want two tensions, so you'll need two equations. One from moments. Is it clear to you what the other is ?

 

[Taniaz]

I'm not really sure what the other is, could you guide me a little please?

 

[Taniaz]

Is it the resultant force? Sum of upward forces= sum of downward forces?

 

[Taniaz]

This is the diagram I drew.

 

[BvU]

Is it the resultant force? Sum of upward forces= sum of downward forces?

Yes. equilibrium means no net force and no net torque.
In the diagram you want to avoid the suggestion that A and B are at the same height. In the cone, the center of mass is on the axis. Now you need the horizontal coordinate for the moments.

 

[Taniaz]

That's what I'm not sure of. How do we find the horizontal coordinates? All we know is that the C.O.M lies at 3/4 h from the vertex and the question doesn't give any other details.

So if I tilt the axis on my diagram so that it's symmetrical then G will lie on the axis-is that what you mean? I don't understand the part about the height being different. If A and B are not at the same height then the cone would no longer be symmetrical?

 

[BvU]

If this is upside down with the vertex below A then B isn't at the same height as A.

All we know is that the C.O.M lies at 3/4 h from the vertex and the question doesn't give any other details

I see what you mean. In such a case, use symbols for unknowns (h, r) and maybe (*) they will cancel in the final result.

(*) Didn't work out the whole thing, so I have to trust the exercise composer in this...

 

[Taniaz]

I think the distance from the c.o.m of the cone to points A and B has to be the radius of the cone. If the height is the same then the coordinates from the c.o.m would be according to me (r, h/4)
and (-r,h/4). If the height is different, we don't even know how different it is so how will we integrate this difference within our equation?

 

[Taniaz]

So I actually made a cone out of paper and hung it in this orientation then traced it onto my notebook. I think even though B is lower than A, the height appears to be the same.

 

[BvU]

2) from post #2

Now it's time to choose a coordinate system and write down some equations.

 

[Taniaz]

Can't we work in Cartesian? Since they don't do polar and cylindrical in A'Levels.
So Ta+Tb=w
and we take the moment around w?

 

[BvU]

We certainly can work in Cartesian. And the axis can be chosen freely.

 

[Taniaz]

So the axis doesn't need to lie on the line of symmetry of the cone?

 

[BvU]

No. You could pick the moments around A (or around the vertex -- same moments) just as well. Choose what you think is easiest.

 

[Taniaz]

I'm afraid I'm still not sure what the coordinates are going to be. I can just think of the radius.

 

[BvU]

Why not start with writing out the two equations for the equilibrium relationships, using symbols for whatever is unknown. Then we can look at those unknowns and try to deal with them...

You already have Ta+Tb=w, so what about these moments ?

 

[Taniaz]

Ok please correct me if I'm wrong.

Ta+Tb=w
and
moment around A (or the vertex) is
w (r)= Tb (2r)
I have a strong feeling it can't be this simple.

 

[BvU]

is (r) the perpendicular distance between W and A ?
(2r) between B and A ?

 

[Taniaz]

No it isn't. So I drew in the perpendicular distance, we can use the Pythogoras theorem but one of the heights is missing. Or can we use similar triangles?

 

[Taniaz]

I've attached the diagram with unknowns

 

[BvU]

I see r and h as before and I also see "x" and "?".

But I also see similar rectangular triangles ...

 

[Taniaz]

x is the perpendicular distance to A from G and ? is the perpendicular distance to A from B? Isn't that correct?
Sorry for the label ? as y
r is the radius of the cone and h is height.

 

[Taniaz]

Maybe I should just give up :(

 

[BvU]

You can always give up, but then you don't have the satisfaction of having found a way through

If the top half angle $\alpha$ of the cone has sine r/h and G is at 3h/4, I know how to calculate x !
And for the perpendicular distance of B and OA you need h and $\sin(2\alpha)$.

[edit] correction: not h but $\sqrt{h^2+r^2}$

Looks a bit messy, but who knows...
Note that h and r are related through W

 

[Taniaz]

Well the x part was simple! *facepalm* thank you!
Where did you get sin (2 alpha) from?

 

[Taniaz]

Oh similar triangles??!

 

[Taniaz]

So this is where I've reached to in solving for the perpendicular distance from B to A but I'm not sure how to simplify this further.

 

[Taniaz]

I think that our sin alpha isn't correct because in the bigger triangle, OA is the hypotenuse which is sqrt of h^2+r^2
So sin α = r / (sqrt of h^2+r^2) for the bigger triangle but
sin α = x / (3/4h) for the smaller triangle since their right angles are at different places.
For the bigger triangle, the right angle is at the centre of the base but the right angle for the smaller triangle is at OA.

 

[Taniaz]

There, all fixed and no complicated equations, everything canceled out nicely. Please let me know if there are any mistakes in this.