JasonHathaway
- 113
- 0
Hi everyone,
I've some points I want to make sure of.
1- When converting a "POINT" from a coordinate system to another, I'll just use the derived equation to convert (e.g. (1,2,3) from cartestian to cylindrical: \rho=\sqrt{x^{2}+y^{2}}, \phi=tan^{-1}\frac{y}{x}, z=z
2- When converting an "EQUATION" (e.g. \sqrt{x^{2}+y^{2}}=\frac{x^{2}y}{y^{2}x}), I'll use the same approach as 1.
3- When converting a "VECTOR" (e.g. 4\vec{i}+3\vec{j}+6\vec{k}), I must convert the unit vector \vec{i}, \vec{j},\vec{k} into their equivalent in my desired coordinate system, whether that vector is A unit vector or not, and I cannot put in the form of a point (e.g. (4,3,6) ) and use the same approach as 1.Okay, and for 3:
a) To convert from cartesian to cylindrical:
Since x=\rho cos(\phi), y=\rho sin(\phi), z=z, then:
\frac{dx}{d \rho}=cos(\phi),\frac{dx}{d \phi}=-\rho sin(\phi), \frac{dx}{dz}=0
\frac{dy}{d \rho}=sin(\phi),\frac{dy}{d \phi}=\rho cos(\phi), \frac{dy}{dz}=0
\frac{dz}{d \rho}=0,\frac{dz}{d \phi}=0, \frac{dz}{dz}=1
And then dot product my vector with each of rho, phi and z components.
But I've found in wikipedia that there's no rho in the derivative with respect to phi...?
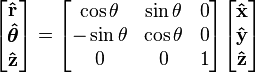
http://en.wikipedia.org/wiki/Vector_fields_in_cylindrical_and_spherical_coordinates
The same thing for the cartesian to spherical.
b) If I want to convert a vector from cylindrical/spherical to cartesian, do I have to take the same approach as a)?
c) How can I convert unit vectors between cylindrical and spherical and vice versa?
I've some points I want to make sure of.
1- When converting a "POINT" from a coordinate system to another, I'll just use the derived equation to convert (e.g. (1,2,3) from cartestian to cylindrical: \rho=\sqrt{x^{2}+y^{2}}, \phi=tan^{-1}\frac{y}{x}, z=z
2- When converting an "EQUATION" (e.g. \sqrt{x^{2}+y^{2}}=\frac{x^{2}y}{y^{2}x}), I'll use the same approach as 1.
3- When converting a "VECTOR" (e.g. 4\vec{i}+3\vec{j}+6\vec{k}), I must convert the unit vector \vec{i}, \vec{j},\vec{k} into their equivalent in my desired coordinate system, whether that vector is A unit vector or not, and I cannot put in the form of a point (e.g. (4,3,6) ) and use the same approach as 1.Okay, and for 3:
a) To convert from cartesian to cylindrical:
Since x=\rho cos(\phi), y=\rho sin(\phi), z=z, then:
\frac{dx}{d \rho}=cos(\phi),\frac{dx}{d \phi}=-\rho sin(\phi), \frac{dx}{dz}=0
\frac{dy}{d \rho}=sin(\phi),\frac{dy}{d \phi}=\rho cos(\phi), \frac{dy}{dz}=0
\frac{dz}{d \rho}=0,\frac{dz}{d \phi}=0, \frac{dz}{dz}=1
And then dot product my vector with each of rho, phi and z components.
But I've found in wikipedia that there's no rho in the derivative with respect to phi...?
http://en.wikipedia.org/wiki/Vector_fields_in_cylindrical_and_spherical_coordinates
The same thing for the cartesian to spherical.
b) If I want to convert a vector from cylindrical/spherical to cartesian, do I have to take the same approach as a)?
c) How can I convert unit vectors between cylindrical and spherical and vice versa?