Lambda96
- 233
- 77
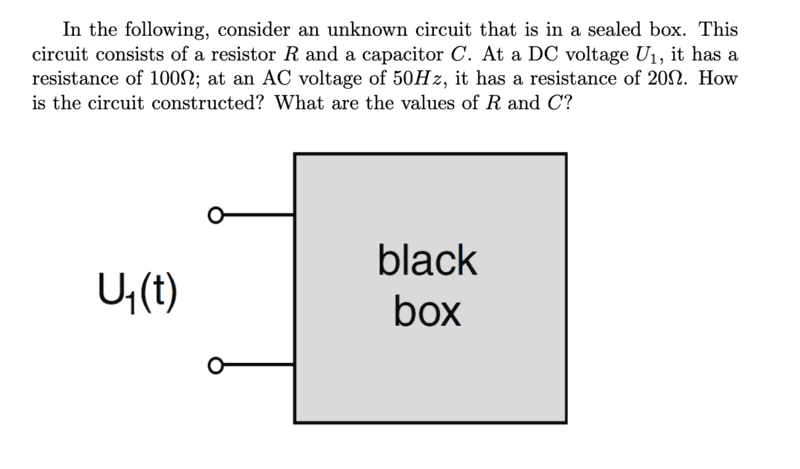
- Homework Statement
- What does the circuit look like and what are the values of resistor ##R## and capacitance ##C##?
- Relevant Equations
- none
Hi,
I am not sure if I have calculated the task correctly
I have now assumed that the capacitor does not need to be charged and is therefore fully charged. In a DC circuit, a capacitor acts like an infinitely large resistor or like an open switch, so I assumed that it is a parallel circuit and that it looks like this.
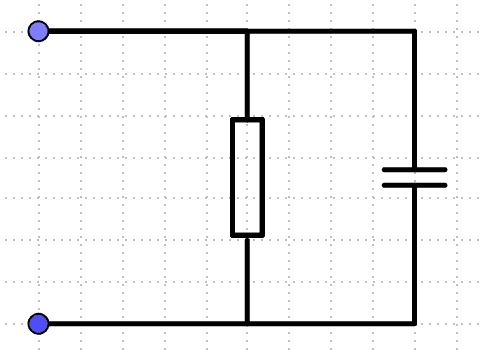
The resistor then has the following value ##R=100 \Omega##.
Using the impedance and the value for ##R##, I can then calculate the value for ##C##.
The value for the impedance in parallel circuit is
$$|Z|=\frac{1}{\sqrt{R^-2+\omega^2 C^2}}$$
##C## can then be calculated as follows
$$C=\frac{R^2-Z^2}{R \omega z}$$
If I now substitute all the values into the above formula, I get the following ##C=9.7 \cdot 10^{-4}F##.
I am not sure if I have calculated the task correctly
I have now assumed that the capacitor does not need to be charged and is therefore fully charged. In a DC circuit, a capacitor acts like an infinitely large resistor or like an open switch, so I assumed that it is a parallel circuit and that it looks like this.
The resistor then has the following value ##R=100 \Omega##.
Using the impedance and the value for ##R##, I can then calculate the value for ##C##.
The value for the impedance in parallel circuit is
$$|Z|=\frac{1}{\sqrt{R^-2+\omega^2 C^2}}$$
##C## can then be calculated as follows
$$C=\frac{R^2-Z^2}{R \omega z}$$
If I now substitute all the values into the above formula, I get the following ##C=9.7 \cdot 10^{-4}F##.