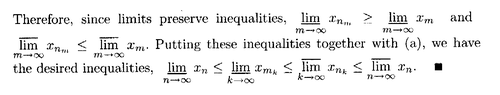Upper and Lower Linits (lim sup and lim inf) - Denlinger, Theorem2.9.6 (b) ....

[Math Amateur]

I am reading Charles G. Denlinger's book: "Elements of Real Analysis".

I am focused on Chapter 2: Sequences ... ...

I need help with the proof of Theorem 2.9.6 (b)Theorem 2.9.6 reads as follows:View attachment 9245
View attachment 9246
In the above proof of part (b) we read the following:

" ... ... Then $$B$$ is an upper bound for every $$n$$-tail of $$\{ x_n \}$$, so $$\overline{ x_n } = \text{sup} \{ x_k \ : \ k \geq n \} \leq B$$. Thus $$\lim_{ n \to \infty } \overline{ x_n } \leq B$$ ... ... "My question is as follows:

Can someone please explain exactly how it follows that $$\lim_{ n \to \infty } \overline{ x_n } \leq B$$ ... that is, how it follows that $$\overline{ \lim_{ n \to \infty } } x_n \leq B$$ ...
(... ... apologies to steep if this is very similar to what has been discussed recently ... )
Hope someone can help ...

Peter
===============================================================================
It may help MHB readers to have access to Denlinger's definitions and notation regarding upper and lower limits ... so I am providing access to the same ... as follows:
View attachment 9247
View attachment 9248Hope that helps ...

Peter

 

[GJA]

Hi Peter,

Can someone please explain exactly how it follows that $$\lim_{ n \to \infty } \overline{ x_n } \leq B$$ ... that is, how it follows that $$\overline{ \lim_{ n \to \infty } } x_n \leq B$$ ...

The newly defined sequence $\left\{\overline{x_{n}}\right\}_{n=1}^{\infty}$ satisfies $\overline{x_{n}}\leq B$ for all $n$. Hence the limit of this sequence cannot exceed the value of $B$. Does this answer your question?

 

[Math Amateur]

Hi Peter,
The newly defined sequence $\left\{\overline{x_{n}}\right\}_{n=1}^{\infty}$ satisfies $\overline{x_{n}}\leq B$ for all $n$. Hence the limit of this sequence cannot exceed the value of $B$. Does this answer your question?

Thanks for the help GJA ...

... your argument gives a plausible account of why $$\overline{ x_n } = \text{sup} \{ x_k \ : \ k \geq n \} \leq B$$ implies that $$\lim_{ n \to \infty } \overline{ x_n } \leq B$$ ... ...

But does your argument constitute an explicit, formal and rigorous argument/proof that a skeptic would accept ...

What do you think ... am I being too extreme or particular ...

Can you help/comment further ...?

Peter

 

[GJA]

A more concrete "proof" would go something like this:

Suppose the limit of the sequence is $L$ and that $L>B$. Let $\varepsilon =\dfrac{L-B}{2}$ and choose $N$ such that $|\overline{x_{n}}-L|<\varepsilon$ for all $n\geq N$. Then $\overline{x_{n}}>L-\varepsilon=\dfrac{L+B}{2}>B$ for all $n\geq N$. This, however, contradicts $\overline{x_{n}}\leq B$ for all $n$.

 

[Math Amateur]

A more concrete "proof" would go something like this:

Suppose the limit of the sequence is $L$ and that $L>B$. Let $\varepsilon =\dfrac{L-B}{2}$ and choose $N$ such that $|\overline{x_{n}}-L|<\varepsilon$ for all $n\geq N$. Then $\overline{x_{n}}>L-\varepsilon=\dfrac{L+B}{2}>B$ for all $n\geq N$. This, however, contradicts $\overline{x_{n}}\leq B$ for all $n$.

Thanks for all your help on this issue GJA ...

Peter