Using Faraday's laws to find the induced EMF

[L_ucifer]

Homework Statement

A circular disk of radius a is rotating at a constant angular speed w in a uniform magnetic field, B, which is directed out of the plane of the page.

Relevant Equations

\epsilon = \frac{d\Phi } {dt} = BAcos(\theta )

Here is the question:

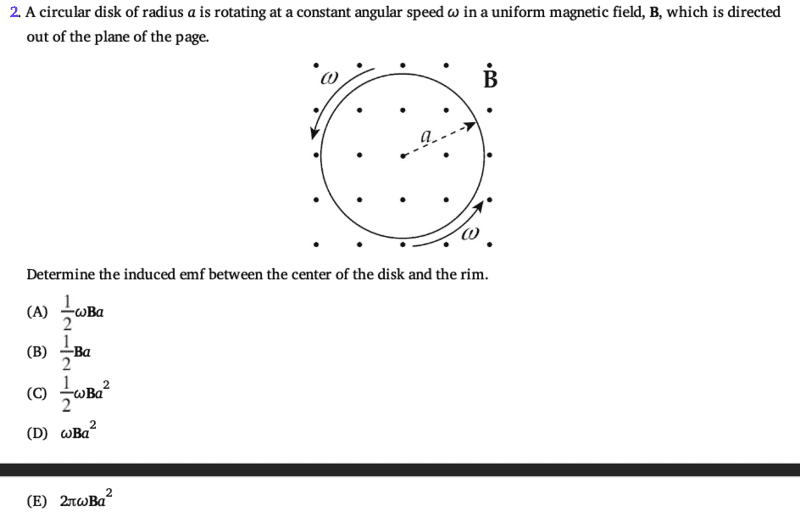
We know the equation \epsilon = \frac{d\phi }{dt} = BAcos(\theta ). This means that the only way we can create an induced voltage is if we change the magnetic field, change the area of the loop in the magnetic field, or change the angle between the normal vector to the surface of the loop and the magnetic field. In this question, neither of those things are changing. Why would there still be induced emf?

 

[Orodruin]

\epsilon = \frac{d\Phi } {dt} = BAcos(\theta )

This is true for the EMF around a closed loop. You are being asked for the EMF between the rim and the center of the disc. Since these are spatially separated, there is no closed loop here.

Edit: A lot of the answers can also be discarded solely based on dimensional analysis.

 

[L_ucifer]

This is true for the EMF around a closed loop. You are being asked for the EMF between the rim and the center of the disc. Since these are spatially separated, there is no closed loop here.

Edit: A lot of the answers can also be discarded solely based on dimensional analysis.

That makes sense, thanks.

 

[Delta2]

Still Faraday's law can be used to calculate the EMF here but we got to have a little imagination on what exactly is the closed loop: Consider a radius of the disk. Then as the disk rotates, imagine that this radius rotate too and the closed loop is the cyclic sector that has the initial position of the radius, the final position of the radius and the in between part of the circumference of disk. Calculate the rate of change of the area of this closed loop as the radius rotate and multiply it by B the intensity of magnetic field..