kirito
- 77
- 9
Thread moved from the technical forums to the schoolwork forums
TL;DR Summary: orbital speed laws
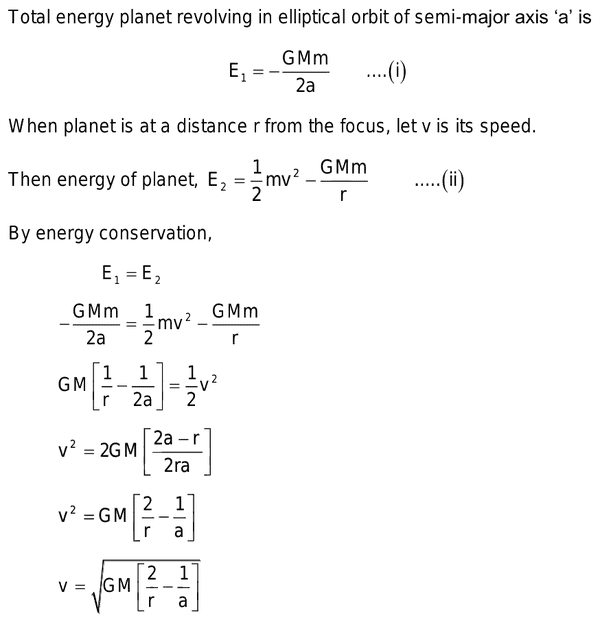
I would appreciate a bit of explanation on how did we find e1 and e2 and if there are any useful references to learn about Kepler laws since I am lost for the most part, and would like to gain understanding and solving ability
,and if you can go into some details on how to know when there is a conservation of momentum and energy
I would appreciate a bit of explanation on how did we find e1 and e2 and if there are any useful references to learn about Kepler laws since I am lost for the most part, and would like to gain understanding and solving ability
,and if you can go into some details on how to know when there is a conservation of momentum and energy