Find the location knowing the resonance using Kepler's third law

  • Thread starter Kovac
  • Start date
  • Tags
    Resonance
  • #1
Kovac
13
2
Thread moved from the technical forums to the schoolwork forums
TL;DR Summary: .

I need to find the location of following bodies MMR with Jupiter: 4:1, 3:1, with the help of Keplers third law.Keplers third law:
1697974988128.png
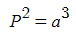, where P is the orbital period in Earth years, a= semi major axis in AU.
For Jupiter: Pj =
1697975054421.png
years.

Now my question is, to find the location of 4:1, should I simply take 1/4 * Pj as the new P? (Since 4 orbits are made with each Jupiter orbit)
And then use the formula again with
1697974988128.png
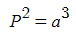to find the position for a? Meaning I need to solve for a with the new P?
 
Physics news on Phys.org
  • #2
I'd think a bit about units/dimensions first! How can a time squared equal a length cubed?
 
  • #3
Could you explain in words what this phrase means?
Kovac said:
MMR with Jupiter: 4:1, 3:1,
Such as: to what variables do the 4:1 and 3:1 apply, and in which direction?

Cheers,
Tom
 

FAQ: Find the location knowing the resonance using Kepler's third law

What is Kepler's third law?

Kepler's third law states that the square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit. Mathematically, it is expressed as \( T^2 \propto a^3 \), where \( T \) is the orbital period and \( a \) is the semi-major axis.

How can Kepler's third law be used to find the location of a celestial object?

By determining the orbital period of a celestial object and using Kepler's third law, one can calculate the semi-major axis of its orbit. This semi-major axis helps in locating the object's average distance from the central body it orbits around, such as a star or planet.

What is resonance in the context of celestial mechanics?

Resonance in celestial mechanics occurs when two orbiting bodies exert regular, periodic gravitational influence on each other, typically because their orbital periods are related by a ratio of small integers. This can lead to increased stability or instability in their orbits.

How does resonance help in determining the location of a celestial object?

Resonance can provide clues about the relative positions and distances of celestial objects. By identifying resonant relationships (e.g., a 2:1 resonance), one can infer the semi-major axes of the orbits involved, thus helping to determine the objects' locations.

What data is needed to apply Kepler's third law and resonance for locating a celestial object?

To apply Kepler's third law and resonance, you need the orbital period of the celestial object and the mass of the central body it orbits. If dealing with resonance, you also need the orbital periods of the other resonant bodies to establish the resonant relationship.

Similar threads

Using Kepler's laws to calculate elliptical planetary motion
Replies
7
Views
525
Kepler's Third Law vs Conservation of angular momentum
Replies
8
Views
2K
Some homework questions in astrophysics (Kepler's Laws, Newton's Laws)
Replies
6
Views
1K
Semi major axis - planetary Science
Replies
1
Views
1K
What is the R^3 in Kepler's 3rd Law?
Replies
7
Views
2K
Kepler's Law to Determine Period of Asteroid
Replies
1
Views
1K
Mass of Jupiter using its moon Sinope
Replies
7
Views
6K
Kepler's Third Law and Motion of Two Point Masses
Replies
8
Views
1K
Kepler's Law for finding velocity
Replies
9
Views
2K
Kepler's Law of Periods and Jupter's Mass
Replies
1
Views
3K

Hot Threads

Recent Insights

Back
Top