Using Kirchhoff's Rule - Theory question

[Sunwoo Bae]

Homework Statement

.

Relevant Equations

.

In my lecture, it was explained that Kirchhoff's Rule is used when circuits are too "complicated" to simplify by combining resistances in series and parallel.

I do not understand in which cases I can simplify circuits by combining resistances, and on which cases I can only use Kirchoff's Rule.

For instance, there are two examples:

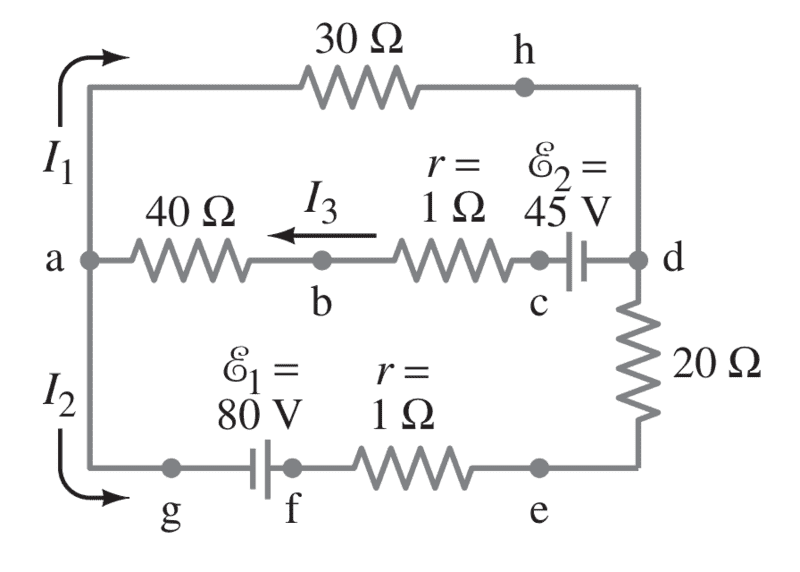
(circuit A - ignore the currents drawn)

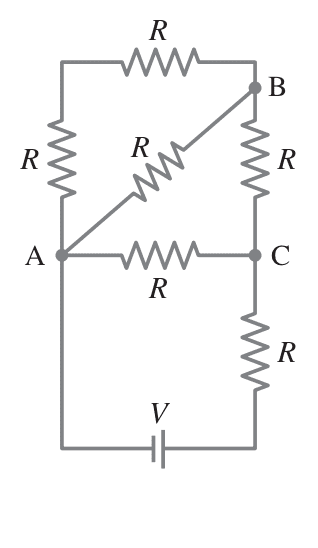
(circuit b)

Circuit a can be ony simplified using Kirchhoff's Rule, while you can use simple combining to find Req of circuit b.
What exactly is different about those two circuits?

Thank you!

 

[Doc Al]

As I'm sure you realize, you can always use Kirchhoff's laws (loop and junction). In circuit b, you can find simple configurations of resistances in series and in parallel. Thus you can simplify some of the analysis in that circuit by replacing those configurations with their equivalent resistance. (Unfortunately, since all the resistors are labeled simply "R", it's hard to discuss those configurations.)

 

[Sunwoo Bae]

As I'm sure you realize, you can always use Kirchhoff's laws (loop and junction). In circuit b, you can find simple configurations of resistances in series and in parallel. Thus you can simplify some of the analysis in that circuit by replacing those configurations with their equivalent resistance. (Unfortunately, since all the resistors are labeled simply "R", it's hard to discuss those configurations.)

Thank you for your reply. But why doesn't the series/parallel rule work for circuit a?

 

[Doc Al]

But why doesn't the series/parallel rule work for circuit a?

It does, at least somewhat. What you are looking for is clean examples of resistor combinations (and nothing else) between two nodes. So, in circuit a you can find: (1) two resistors in series between nodes a and c; (2) two resistors in series between nodes d and f. Depending on what you need to find, that may or may not be useful.

 

[Sunwoo Bae]

It does, at least somewhat. What you are looking for is clean examples of resistor combinations (and nothing else) between two nodes. So, in circuit a you can find: (1) two resistors in series between nodes a and c; (2) two resistors in series between nodes d and f. Depending on what you need to find, that may or may not be useful.

So if you are looking, for instance, Req in circuit a, would it be possible to do so solely using the series/parallel simplification?

 

[Doc Al]

So if you are looking, for instance, Req in circuit a, would it be possible to do so solely using the series/parallel simplification?

I'm not sure what you mean, but I think the answer is "no".

The "trick" is always to look for combinations that can be replaced by their equivalents (as mentioned above) and then see where you are. The fact that there are several voltage sources limits that simplification.

 

[Doc Al]

Since circuit B has a single voltage source, you can keep simplifying until you have just a single equivalent resistance with that voltage across it. (Assuming that gives you what you need for a given problem.)

 

[Steve4Physics]

Circuit a can be ony simplified using Kirchhoff's Rule, while you can use simple combining to find Req of circuit b.
What exactly is different about those two circuits?

To use the ‘series/parallel’ method you essentially need to reduce the circuit to an equivalent circuit containing one cell and one resistor. That then gives the current through the cell so you can ‘work backwards’, finding voltages and currents for the components in the original circuit.

This works fine for circuit b.

In circuit a you can:
a) replace the 40Ω and the middle 1Ω by a single 41Ω resistor;
b) replace the 20Ω and the lower 1Ω by a single 21Ω resistor.

You are then left with the equivalent circuit containing three resistors (30Ω, 41Ω and 21Ω) and 2 cells.

The three resistors are not in series or parallel because of the positions of the cells. And the cells are not in series so can’t be combined into a single cell. So you can't take the analysis any further using the ‘series/parallel’ method

 

[Sunwoo Bae]

Understood! Thank you for your replies!