Sunwoo Bae
- 60
- 4
- Homework Statement
- .
- Relevant Equations
- .
In my lecture, it was explained that Kirchhoff's Rule is used when circuits are too "complicated" to simplify by combining resistances in series and parallel.
I do not understand in which cases I can simplify circuits by combining resistances, and on which cases I can only use Kirchoff's Rule.
For instance, there are two examples:
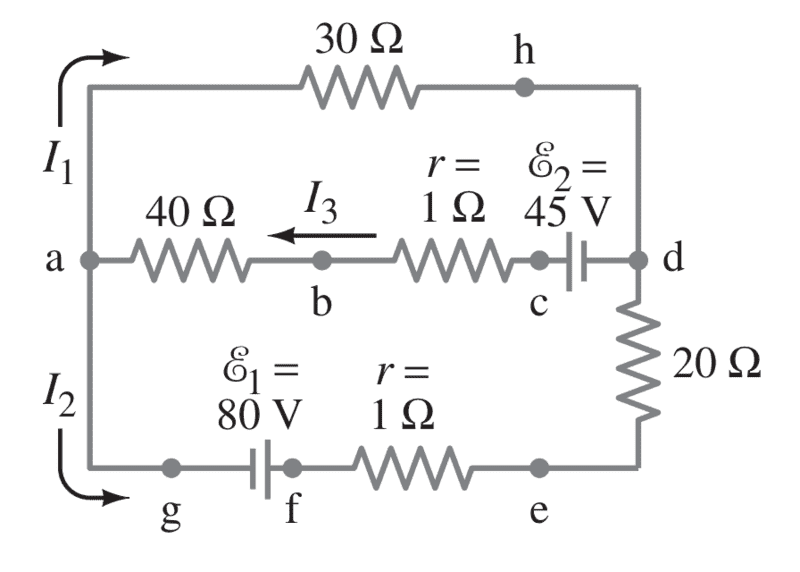
(circuit A - ignore the currents drawn)
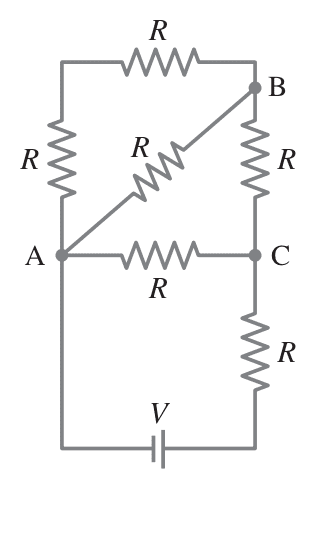
(circuit b)
Circuit a can be ony simplified using Kirchhoff's Rule, while you can use simple combining to find Req of circuit b.
What exactly is different about those two circuits?
Thank you!
I do not understand in which cases I can simplify circuits by combining resistances, and on which cases I can only use Kirchoff's Rule.
For instance, there are two examples:
(circuit A - ignore the currents drawn)
(circuit b)
Circuit a can be ony simplified using Kirchhoff's Rule, while you can use simple combining to find Req of circuit b.
What exactly is different about those two circuits?
Thank you!