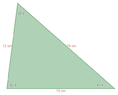
To follow up:
We have:
$$\frac{\sin(\theta)}{2x}=\frac{\sin(2\theta)}{3x}$$
Multiplying through by \(6x\) and using a double-angle identity we obtain:
$$3\sin(\theta)=4\sin(\theta)\cos(\theta)$$
As presumably \(\sin(\theta)\ne0\) (otherwise our triangle is degenerate) we may divide by this quantity to get:
$$3=4\cos(\theta)\implies \cos(\theta)=\frac{3}{4}$$
And so the 3 interior angles are:
$$\theta=\arccos\left(\frac{3}{4}\right)$$
$$2\theta=2\arccos\left(\frac{3}{4}\right)$$
$$\pi-3\arccos\left(\frac{3}{4}\right)$$
As these 3 angles are different, we know we have a scalene triangle, and knowing this will help.
Now, let's use the Law of Cosines as follows:
$$(2x)^2=(3x)^2+15^2-2(3x)(15)\cos(\theta)$$
$$4x^2=9x^2+15^2-90x\left(\frac{3}{4}\right)$$
Arrange resulting quadratic in standard form:
$$2x^2-27x+90=0$$
Factor:
$$(2x-15)(x-6)=0$$
Because \(2x\) cannot be 15 as all three sides must have different lengths, we reject that root and are left with:
$$x=6$$
And so, our triangle has:
Side \(a\) is 12 cm and the angle opposing it is about $$41.4^{\circ}$$.
Side \(b\) is 18 cm and the angle opposing it is about $$82.8^{\circ}$$.
Side \(c\) is 15 cm and the angle opposing it is about \(55.8^{\circ}\).
View attachment 9699