Comp Sci Using Single Source Shortest Path Algorithm to find the longest path

[Monsterboy]

Homework Statement

Using Single Source Shortest Path Algorithm to find the longest path

Relevant Equations

First multiply the edge weights by -1 and find the shortest path, then multiply the result by -1 again.

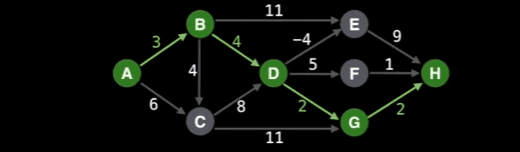
This is the weighted, directed acyclic graph I created in JavaScript

class WeightedDirectedGraph {
constructor() {
this.adjacencyList = {};
}

addNode(node) {
if(!this.adjacencyList[node]) {
this.adjacencyList[node] = [];
}
}

addEdge(node1, node2, direction, weight) {
this.adjacencyList[node1].push({node: node2, direction: direction, weight: weight });
this.adjacencyList[node2].push({node: node1, direction: direction, weight: weight });
}

getEdgesFromNode(node) {
let edges = []
if(this.adjacencyList[node]) {
for (let i = 0; i < this.adjacencyList[node].length; i++) {
edges.push(this.adjacencyList[node][i]);
}
}
return edges;
}
}

let graph = new WeightedDirectedGraph();
graph.addNode("A")
graph.addNode("B")
graph.addNode("C")
graph.addNode("D")
graph.addNode("E")
graph.addNode("F")
graph.addNode("G")
graph.addNode("H")

graph.addEdge("A", "B", {from: "A", to: "B"}, 3)
graph.addEdge("A", "C", {from: "A", to: "C"}, 6)
graph.addEdge("B", "C", {from: "B", to: "C"}, 4)
graph.addEdge("B", "D", {from: "B", to: "D"}, 4)
graph.addEdge("B", "E", {from: "B", to: "E"}, 11)
graph.addEdge("C", "D", {from: "C", to: "D"}, 8)
graph.addEdge("C", "G", {from: "C", to: "G"}, 11)
graph.addEdge("D", "E", {from: "D", to: "E"}, -4)
graph.addEdge("D", "F", {from: "D", to: "F"}, 5)
graph.addEdge("D", "G", {from: "D", to: "G"}, 2)
graph.addEdge("E", "H", {from: "E", to: "H"}, 9)
graph.addEdge("F", "H", {from: "F", to: "H"}, 1)
graph.addEdge("G", "H", {from: "G", to: "H"}, 2)

I will attach an image to visualize this graph

This is the topological sort code

function topSort(graph) {
let N = Object.keys(graph.adjacencyList).length
let V = {};  // visited nodes list
let ordering = [];
for (let node in graph.adjacencyList) {
V[node] = false;
ordering.push(0);
}
let i = N - 1;
for (let node in graph.adjacencyList) {
if(V[node] === false) {
i = dfs(i, node, V, ordering, graph)
}
}
return ordering;
}

function dfs(i, node, V, ordering, graph) {
V[node] = true;
let edges = graph.getEdgesFromNode(node)
for (let k = 0; k < edges.length; k++) {
if (V[edges[k].direction.to] === false) {
i = dfs(i, edges[k].direction.to, V, ordering, graph)
}
}
ordering[i] = node;
return i - 1;
}

function dagShortestPath(graph, startNode) {
let topSortResult = topSort(graph);
let distances = {};
topSortResult.forEach((node) => {
distances[node] = Infinity;
})

distances[startNode] = 0;
for( let i = 0; i < topSortResult.length; i++) {
let nodeIndex = topSortResult[i];
let edges = graph.getEdgesFromNode(nodeIndex);
if (edges.length !== 0) {
let newDist;
for (let i = 0; i < edges.length; i++) {
newDist = distances[nodeIndex] + edges[i].weight;
if (distances[edges[i].direction.to] === Infinity) {
distances[edges[i].direction.to] = newDist;
}
else if (newDist > -1) {
distances[edges[i].direction.to] = Math.min(distances[edges[i].direction.to], newDist);
}
}
}
}
return distances;
}

I tested the code for the shortest path from node A to all other nodes, I am getting it right.
The output is { A: 0, B: 3, C: 6, D: 7, G: 9, F: 12, E: 3, H: 11 }

This is the code for the longest path.

function LongestPath(graph, startNode) {
  let topSortResult = topSort(graph);
  let distances = {};
  topSortResult.forEach((node) => {
    distances[node] = Infinity;
  })
  distances[startNode] = 0;
  // multiply all edge weights by -1
  for (let node in graph.adjacencyList) {
    for (let i = 0; i < graph.adjacencyList[node].length; i++) {
      graph.adjacencyList[node][i].weight = graph.adjacencyList[node][i].weight*-1;
    }
  }
  console.log(graph.adjacencyList);
  let longestDistances = dagShortestPath(graph, startNode);
// multiply all edge weights by -1 after getting longest path
for (let node in graph.adjacencyList) {
  for (let i = 0; i < graph.adjacencyList[node].length; i++) {
    graph.adjacencyList[node][i].weight = graph.adjacencyList[node][i].weight*-1;
  }
}
  for (let node in longestDistances) {
    longestDistances[node] *= -1;
  }
  return longestDistances;
}

I am getting this wrong, even though the only change is the multiplication of the edge weights with -1.
Output is { A: -0, B: 3, C: 6, D: 7, G: 17, F: 12, E: 14, H: 19 } although for some nodes the output is right.

I took the image and the idea of multiplying by -1 from this free YouTube course on graph algorithms from freeCodeCamp.org channel -

Algorithms Course - Graph Theory Tutorial from a Google Engineer​

 

[pbuk]

If you set the language to javascript as in the code below it is much easier to read.

class WeightedDirectedGraph {
constructor() {
this.adjacencyList = {};
}

addNode(node) {
if(!this.adjacencyList[node]) {
this.adjacencyList[node] = [];
}
}

addEdge(node1, node2, direction, weight) {
this.adjacencyList[node1].push({node: node2, direction: direction, weight: weight });
this.adjacencyList[node2].push({node: node1, direction: direction, weight: weight });
}

getEdgesFromNode(node) {
let edges = []
if(this.adjacencyList[node]) {
for (let i = 0; i < this.adjacencyList[node].length; i++) {
edges.push(this.adjacencyList[node][i]);
}
}
return edges;
}
}

let graph = new WeightedDirectedGraph();
graph.addNode("A")
graph.addNode("B")
graph.addNode("C")
graph.addNode("D")
graph.addNode("E")
graph.addNode("F")
graph.addNode("G")
graph.addNode("H")

graph.addEdge("A", "B", {from: "A", to: "B"}, 3)
graph.addEdge("A", "C", {from: "A", to: "C"}, 6)
graph.addEdge("B", "C", {from: "B", to: "C"}, 4)
graph.addEdge("B", "D", {from: "B", to: "D"}, 4)
graph.addEdge("B", "E", {from: "B", to: "E"}, 11)
graph.addEdge("C", "D", {from: "C", to: "D"}, 8)
graph.addEdge("C", "G", {from: "C", to: "G"}, 11)
graph.addEdge("D", "E", {from: "D", to: "E"}, -4)
graph.addEdge("D", "F", {from: "D", to: "F"}, 5)
graph.addEdge("D", "G", {from: "D", to: "G"}, 2)
graph.addEdge("E", "H", {from: "E", to: "H"}, 9)
graph.addEdge("F", "H", {from: "F", to: "H"}, 1)
graph.addEdge("G", "H", {from: "G", to: "H"}, 2)

And if you add indentation it is easier still:

class WeightedDirectedGraph {
  constructor() {
    this.adjacencyList = {};
  }

  addNode(node) {
    if(!this.adjacencyList[node]) {
      this.adjacencyList[node] = [];
    }
  }

  addEdge(node1, node2, direction, weight) {
    this.adjacencyList[node1].push({ node: node2, direction: direction, weight: weight });
    this.adjacencyList[node2].push({ node: node1, direction: direction, weight: weight });
  }

  getEdgesFromNode(node) {
    let edges = []
    if(this.adjacencyList[node]) {
      for (let i = 0; i < this.adjacencyList[node].length; i++) {
        edges.push(this.adjacencyList[node][i]);
      }
    }
    return edges;
  }
}

This bug might be hard to track down. I suggest you focus on what each line of code is doing when it decides that the longest path from A to C is 6 instead of 7 as this is the simplest "error".

 

[Monsterboy]

Is the idea of multiplying the edge weights by -1 to find the longest path right ? Does it actually work ?

 

[Monsterboy]

In the graph class definition, this method was returning wrong edges.

 getEdgesFromNode(node) {
    let edges = []
    if(this.adjacencyList[node]) {
      for (let i = 0; i < this.adjacencyList[node].length; i++) {
        if(this.adjacencyList[node][i].direction.from === node) {   // this condition fixed the issue.
          let edge = {direction: this.adjacencyList[node][i].direction, weight: this.adjacencyList[node][i].weight}
          edges.push(edge);  
        }
      }
    }
    return edges; 
  }

 

[pbuk]

In the graph class definition, this method was returning wrong edges.

Glad you tracked it down, well done.