##\vec v## and ##\vec a## expressions - motion on an off center circle

[Like Tony Stark]

Homework Statement

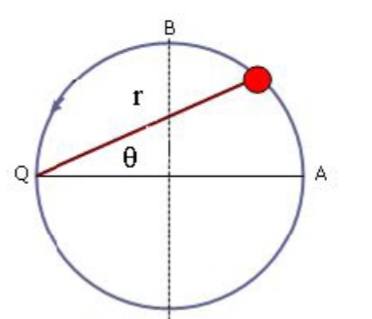
A particle moves along a circular trajectory, and its angular coordinate depends on $q(t)=0,8t$. Considering $Q$ as the origin, find the expressions for velocity and acceleration in function of time, and also their radial and angular components.

Relevant Equations

$\dot{r} = \dot{r} e_r + r \dot{\theta} e_\theta$
$\ddot{x} = (\ddot{r}-r \dot{\theta}^2) e_r + (r \ddot{\theta}+2 \dot{r} \dot{\theta}) e_\theta$

Well, I tried decomposing velocity into its components on the radial and angular axis. But I have problems with the angles because in some parts of the trajectory the velocity is on the angular coordinate, but in other parts it isn't. I mean, I can't say $V=V e_\theta$ because it's not always like that. So I'm having problems finding out which trigonometric relationship should I use to be able to decompose it.

 

[Charles Link]

It's unclear how you worded the problem in the OP what $q(t)$ is. The problem probably is somewhat routine, but I can't follow what $q(t)=0,8t$ means.